
 設函數y=(x+1)[(k-2)x+(2k-3)](k是常數).
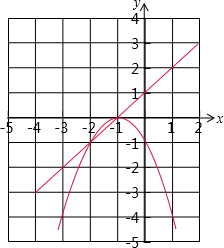
設函數y=(x+1)[(k-2)x+(2k-3)](k是常數).分析 (1)把k=3代入y=(x+1)[(k-2)x+(2k-3)]得到y=x2+4x+3,配方得到y=(x+2)2-1,所以函數y3的對稱軸為直線x=-2,頂點坐標為(-2,-1),然后利用描點法畫出函數y3的圖象;
(2)利用函數圖象經過固定點進行回答;
(3)利用點平移的規律得到點(-2,-1)平移所得對應點的坐標為(-4,-5),然后根據頂點式寫出y4的解析式,然后根據二次函數的性質確定函數y4的最小值.
解答 解:(1)當k=3時,y3=(x+1)(x+3)=x2+4x+3=(x+2)2-1,
則函數y3的對稱軸為直線x=-2,頂點坐標為(-2,-1),
如圖,
(2)①圖象都經過(-2,-1)和(-1,0);
②圖象總交x軸于點(-1,0);
(3)函數y3的對稱軸為直線x=-2,頂點坐標為(-2,-1),把點(-2,-1)向左平移2個單位,再向下平移4個單位所得對應點的坐標為(-4,-5),
所以函數y4的解析式為y=(x+4)2-5,
當x取-4時,函數y4的最小值是-5.
點評 本題考查了二次函數圖象與幾何變換:由于拋物線平移后的形狀不變,故a不變,所以求平移后的拋物線解析式通常可利用兩種方法:一是求出原拋物線上任意兩點平移后的坐標,利用待定系數法求出解析式;二是只考慮平移后的頂點坐標,即可求出解析式.也考查了二次函數的圖象.


 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:初中數學 來源: 題型:填空題
 如圖,正方形ABCD的邊長為6,點E是AB上的一點,將△BCE沿CE折疊至△FCE,若CF,CE恰好與以正方形ABCD的中心為圓心的⊙O相切,則折痕CE=4$\sqrt{3}$.
如圖,正方形ABCD的邊長為6,點E是AB上的一點,將△BCE沿CE折疊至△FCE,若CF,CE恰好與以正方形ABCD的中心為圓心的⊙O相切,則折痕CE=4$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
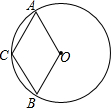 如圖,四邊形ABCO中,點A,B,C在劣弧$\widehat{AB}$上,則下列結論正確的有①②④(在橫線上填寫所有正確結論的序號).
如圖,四邊形ABCO中,點A,B,C在劣弧$\widehat{AB}$上,則下列結論正確的有①②④(在橫線上填寫所有正確結論的序號).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 營業員 | 小張 | 小王 |
| 月銷售件數 | 200 | 150 |
| 月總收入/元 | 1400 | 1250 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,是一個正方體紙盒展開圖,按虛線折成正方體后,若使相對面上的兩數互為相反數,則A、B、C表示的數依次是-5,-π,$\frac{3}{2}$.
如圖,是一個正方體紙盒展開圖,按虛線折成正方體后,若使相對面上的兩數互為相反數,則A、B、C表示的數依次是-5,-π,$\frac{3}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com