
分析 (1)連接CM,構造Rt△COM,利用勾股定理可求得結論;
(2)假設存在這樣的點P,根據題意,可知△CMP為等腰直角三角形,且CM=MP=5,根據圓的方程和兩點直接的距離公式列出方程組,解之即可得出點P的坐標;
(3)作MH⊥AN于H,則AH=NH,易證△AMH≌△MCO,故AH=MO,由垂徑定理可證得結論.
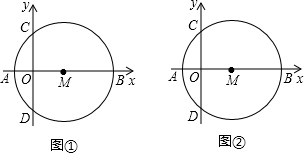
解答  解:(1)如圖①,連接CM,
解:(1)如圖①,連接CM,
在Rt△COM中,OC=4,OM=3,CM=$\sqrt{O{C}^{2}+O{M}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴AM=5,
∴OA=2,
∴⊙M的半徑為5,A(-2,0);
(2)假設存在這樣的點P(x,y),結合題意,
可得△CMP為等腰直角三角形,且CM=PM=5,
故CP=5$\sqrt{2}$;
結合題意有,
$\left\{\begin{array}{l}{(x-3)^{2}+{y}^{2}=25}\\{{x}^{2}+(y-4)^{2}=50}\end{array}\right.$;
解之得:
$\left\{\begin{array}{l}{{x}_{1}=7}\\{{y}_{1}=3}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-3}\end{array}\right.$,
即存在兩個這樣的點P;
P1(7,3),P2(-1,-3);
(3)證明:如圖2,連接CM,作MH⊥AN于H,
則AH=HN,
∵EC切⊙M,
∴∠ECM=90°,
∴四邊形DMCF是矩形,
∴∠CMH=90°,
在△AMH和△MCO中,
$\left\{\begin{array}{l}{∠CMO=∠MAH=90°-∠AMH}\\{∠COM=∠ADM=90°}\\{CM=AM}\end{array}\right.$
∴△AMH≌△MCO,
∴AH=M0=3,
即AN=HN+AH=3+3=6.
點評 本題主要考查的是垂徑定理的應用和切線與圓之間的性質關系,勾股定理,全等三角形的判定與性質,矩形的判定與性質,等腰直角三角形的性質,方程組的解法,綜合性強,能夠熟練掌握垂徑定理的應用和切線與圓之間的性質關系是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
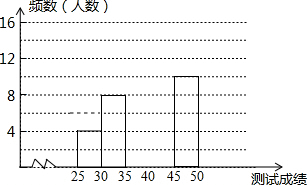 某校九年級舉辦了首屆“漢字聽寫大賽”,全校500名九年級學生全部參加,他們同時聽寫50個漢字,每正確聽寫出一個漢字得1分,為了解學生們的成績,隨機抽取了部分學生的成績,并根據測試成績繪制出如下兩幅不完整的統計表和頻數分布直方圖:
某校九年級舉辦了首屆“漢字聽寫大賽”,全校500名九年級學生全部參加,他們同時聽寫50個漢字,每正確聽寫出一個漢字得1分,為了解學生們的成績,隨機抽取了部分學生的成績,并根據測試成績繪制出如下兩幅不完整的統計表和頻數分布直方圖:| 組別 | 成績x分 | 人數 | 頻率 |
| 1組 | 25≤<30 | 4 | 0.08 |
| 2組 | 30≤x<35 | 8 | 0.16 |
| 3組 | 35≤x<40 | a | 0.32 |
| 4組 | 40≤x<45 | b | c |
| 5組 | 45≤x<50 | 10 | 0.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
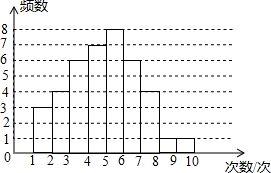 為了解我市某中學九年級學生的體能情況,在該校800名九年級學生中隨機抽取了部分學生進行引體向上測試,現對這部分學生引體向上的次數進行統計,并繪制成如圖所示的頻數分布直方圖.
為了解我市某中學九年級學生的體能情況,在該校800名九年級學生中隨機抽取了部分學生進行引體向上測試,現對這部分學生引體向上的次數進行統計,并繪制成如圖所示的頻數分布直方圖.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
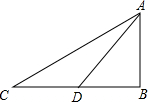 如圖,從地面上C、D兩處望山頂A,仰角分別為30°和45°,若C、D兩處相距200米,則山高AB為( )
如圖,從地面上C、D兩處望山頂A,仰角分別為30°和45°,若C、D兩處相距200米,則山高AB為( )| A. | 100($\sqrt{3}$+1)米 | B. | 100米 | C. | 100$\sqrt{2}$ | D. | 200$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com