
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | $\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$ | C. | $\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$ | D. | 3,4,6 |
分析 欲求證是否為直角三角形,這里給出三邊的長,只要驗證兩小邊的平方和等于最長邊的平方即可.
解答 解:A、($\sqrt{3}$)2+22≠($\sqrt{5}$)2,不能構成直角三角形;
B、($\sqrt{1}$)2+($\sqrt{2}$)2=($\sqrt{3}$)2,能構成直角三角形;
C、($\sqrt{6}$)2+($\sqrt{8}$)2≠($\sqrt{10}$)2,不能構成直角三角形;
D、32+42≠62,不能構成直角三角形.
故選B.
點評 本題考查勾股定理的逆定理的應用.判斷三角形是否為直角三角形,已知三角形三邊的長,只要利用勾股定理的逆定理加以判斷即可.勾股定理的逆定理:若三角形三邊滿足a2+b2=c2,那么這個三角形是直角三角形.


 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:選擇題
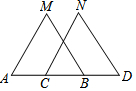 如圖,在△ABM和△CDN中,A,C,B,D在同一條直線上,MB=ND,MA=NC,則下列條件中能判定△ABM≌△CDN的是( )
如圖,在△ABM和△CDN中,A,C,B,D在同一條直線上,MB=ND,MA=NC,則下列條件中能判定△ABM≌△CDN的是( )| A. | ∠MAB=∠NCD | B. | ∠MBA=∠NDC | C. | AC=BD | D. | AM∥CN |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 小貓在如圖所示的地面上自由地走來走去,并隨意停留在某塊方磚上(圖中每一塊方磚除顏色外完全相同),小貓的大小忽略不計,則小貓停留在白色方磚上的概率是$\frac{5}{8}$.
小貓在如圖所示的地面上自由地走來走去,并隨意停留在某塊方磚上(圖中每一塊方磚除顏色外完全相同),小貓的大小忽略不計,則小貓停留在白色方磚上的概率是$\frac{5}{8}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com