
分析 分①以AC=5為軸旋轉一周和②以BC=12為軸旋轉一周兩種情況,先得出圓錐的底面圓的半徑及母線長,根據S=$\frac{1}{2}$•2πr•L可得答案.
解答 解:①若以AC=5為軸旋轉一周,
則圓錐的底面半徑為BC=12,母線AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∴斜邊AB形成的圓錐的側面積為$\frac{1}{2}$×2π×12×13=156π;
②若以BC=12為軸旋轉一周,
則圓錐的底面半徑為AC=5,母線AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∴斜邊AB形成的圓錐的側面積為$\frac{1}{2}$×2π×5×13=65π.
點評 本題主要考查圓錐的計算、勾股定理及旋轉體,根據題意分類討論得出旋轉所得幾何體的底面圓的半徑及母線長是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在矩形ABCD中,AB=12cm,BC=6cm,點P沿AB邊從A向B以2cm/s的速度移動;點Q沿DA邊從D向A以1cm/s的速度移動.如果P,Q同時出發,用t(s)表示移動時間(0≤t≤6),那么:
如圖,在矩形ABCD中,AB=12cm,BC=6cm,點P沿AB邊從A向B以2cm/s的速度移動;點Q沿DA邊從D向A以1cm/s的速度移動.如果P,Q同時出發,用t(s)表示移動時間(0≤t≤6),那么:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
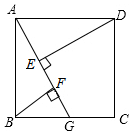 已知:在正方形ABCD中,點G是BC邊上的任意一點,DE⊥AG于點E,BF∥DE,交AG于點F. 求證:
已知:在正方形ABCD中,點G是BC邊上的任意一點,DE⊥AG于點E,BF∥DE,交AG于點F. 求證:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com