

分析 (1)根據碟寬的定義以及等腰直角三角形的性質可以假設B(m,m),代入拋物線的解析式,求出A、B兩點坐標即可解決問題.
(2)利用(1)中結論碟寬為$\frac{2}{a}$,列出方程即可解決問題.
(3)①由F2的碟寬:F1的碟寬=1:2,即$\frac{2}{{a}_{2}}$:$\frac{2}{{a}_{1}}$=1:2,由a1=$\frac{1}{3}$,可得a2=$\frac{2}{3}$,再求出y2的頂點坐標即可解決問題.
②先求出h1,h2,…,B1,B2,…的橫坐標,探究規律后即可解決問題.
解答 解:(1)根據碟寬的定義以及等腰直角三角形的性質可以假設B(m,m).
①把B(m,m)代入y=x2,得到m=1或0(舍棄),
∴A(-1,1),B(1,1),
∴AB=2,即碟寬為2.
②把B(m,m)代入y=$\frac{1}{2}$x2,得到m=2或0(舍棄),
∴A(-2,2),B(2,2),
∴AB=4,即碟寬為4.
③把B(m,m)代入y=ax2,得到m=$\frac{1}{a}$或0(舍棄),
∴A(-$\frac{1}{a}$,$\frac{1}{a}$),B($\frac{1}{a}$,$\frac{1}{a}$),
∴AB=$\frac{2}{a}$,即碟寬為$\frac{2}{a}$.
④根據碟寬的定義以及等腰直角三角形的性質,碟寬的大小與頂點的位置無關,所以$\frac{2}{a}$.
故答案分別為2,4,$\frac{2}{a}$,$\frac{2}{a}$.
(2)由(1)可知碟寬為$\frac{2}{a}$=6,
∴a=$\frac{1}{3}$,
∴拋物線的解析式為y=$\frac{1}{3}$x2-$\frac{4}{3}$x-$\frac{5}{3}$.
(3)①∵y1=$\frac{1}{3}$x2-$\frac{4}{3}$x-$\frac{5}{3}$=$\frac{1}{3}$(x-2)2-3的碟寬AB在x軸上,(A在B左邊),
∴A(-1,0),B(5,0),
∴拋物線y2的頂點坐標為(2,0),
∵F2的碟寬:F1的碟寬=1:2,
∴$\frac{2}{{a}_{2}}$:$\frac{2}{{a}_{1}}$=1:2,
∵a1=$\frac{1}{3}$,
∴a2=$\frac{2}{3}$,
∴拋物線y2的解析式為y=$\frac{2}{3}$(x-2)2.
②∵hn:hn-1=1:2,h1=3,
∴h2=$\frac{3}{2}$,h3=$\frac{3}{{2}^{2}}$,h4=$\frac{3}{{2}^{3}}$,…,hn=$\frac{3}{{2}^{n-1}}$,
點碟寬右端點B的 橫坐標,B1的橫坐標3,B2的橫坐標為3+$\frac{3}{2}$,B3的橫坐標為3+$\frac{3}{{2}^{2}}$,B4的橫坐標為3+$\frac{3}{{2}^{3}}$,…Bn的橫坐標為3+$\frac{3}{{2}^{n-1}}$,
故答案為$\frac{3}{{2}^{n-1}}$,3+$\frac{3}{{2}^{n-1}}$.
點評 本題考查二次函數綜合題,等腰直角三角形的性質、“準碟形”的定義等知識,解題的關鍵是理解題意,靈活運用所學知識解決問題,學會從特殊到一般的探究規律的方法,屬于中考壓軸題.


科目:初中數學 來源: 題型:填空題
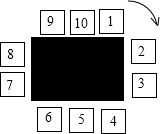 如圖,在一個桌子周圍放置著10個箱子,按順時針方向編為1~10號.小華在1號箱子中投入一顆紅球后,沿著桌子按順時針方向行走,每經過一個箱子就根據下列規則投入一顆球:
如圖,在一個桌子周圍放置著10個箱子,按順時針方向編為1~10號.小華在1號箱子中投入一顆紅球后,沿著桌子按順時針方向行走,每經過一個箱子就根據下列規則投入一顆球:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
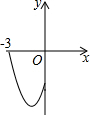 在平面直角坐標系中,二次函數y=x2+2x-3(-3≤x≤0)的圖象如圖所示,點A(x1,y1),B(x2,y2)(x1<x2)是該二次函數圖象上的兩點,則下列結論中錯誤的是②④(填序號)
在平面直角坐標系中,二次函數y=x2+2x-3(-3≤x≤0)的圖象如圖所示,點A(x1,y1),B(x2,y2)(x1<x2)是該二次函數圖象上的兩點,則下列結論中錯誤的是②④(填序號)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 與標準質量的差值(克) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋數(袋) | 1 | 4 | 3 | 4 | 5 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
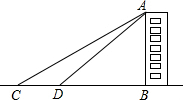 某班開展測量教學樓高度的綜合實踐活動.大家完成任務的方法有很多種,其中一種方法是:如圖,他們在C點測得教學樓AB的頂部點A的仰角為30°,然后向教學樓前進20米到達點D,在點D測得點A的仰角為60°,且B,C,D三點在一條直線上.請你根據這些數據,求出這幢教學樓AB的高度.
某班開展測量教學樓高度的綜合實踐活動.大家完成任務的方法有很多種,其中一種方法是:如圖,他們在C點測得教學樓AB的頂部點A的仰角為30°,然后向教學樓前進20米到達點D,在點D測得點A的仰角為60°,且B,C,D三點在一條直線上.請你根據這些數據,求出這幢教學樓AB的高度.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
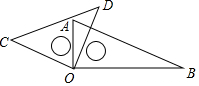 如圖,小明將自己用的一副三角板擺成如圖形狀,下列結論錯誤的是( )
如圖,小明將自己用的一副三角板擺成如圖形狀,下列結論錯誤的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA與∠DOA互余 | D. | ∠AOD與∠COB互補 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com