Question

11．在一個不透明的盒子里裝有5個分別寫有數字-2，-1，1，2，3的小球，它們除數字不同外其余全部相同，現從盒子里隨機取出一個小球，將該小球上的數字作為點P的橫坐標，將該數的絕對值作為點P的縱坐標，則點P落在拋物線y=-x²+2x+4與x軸所圍成的區域內（不含邊界）的概率是$\frac{2}{5}$．

Answer 1

分析 首先根據題意求得所有的點P的坐標，然后求得二次函數與x軸的交點與頂點坐標，畫出圖象；然后分別分析在拋物線y=-x²+2x+4與x軸所圍成的區域內（不含邊界）的情況，再利用概率公式求解即可求得答案．

解答 解：如圖，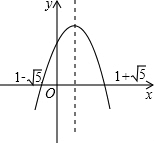
-2，-1，1，2，3的絕對值為2，1，1，2，3．
點P的坐標為（-2，2），（-1，1），（1，1），（2，2），（3，3）；
描出各點：-2＜1-$\sqrt{5}$，不合題意；
把x=-1代入解析式得：y₁=1，1=1，故（-1，1）在邊界上，不在區域內；
把x=1代入解析式得：y₂=5，1＜5，故（1，1）在該區域內；
把x=2代入解析式得：y₃=4，2＜4，故（2，2）在該區域內；
把x=3代入解析式得：y₄=1，1＜3，故（3，3）不在該區域內．
所以5個點中有2個符合題意．
故點P落在拋物線y=-x²+2x+4與x軸所圍成的區域內（不含邊界）的概率是$\frac{2}{5}$．
故答案為：$\frac{2}{5}$．

點評 此題考查了二次函數的性質，概率公式的應用以及絕對值的定義．此題難度適中，解題的關鍵是注意數形結合思想的應用．