
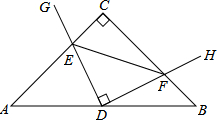
 在Rt△ABC中,AC=BC,點D為AB中點.∠GDH=90°,∠GDH繞點D旋轉,DG、DH分別與邊AC、BC交于E,F兩點.下列結論:
在Rt△ABC中,AC=BC,點D為AB中點.∠GDH=90°,∠GDH繞點D旋轉,DG、DH分別與邊AC、BC交于E,F兩點.下列結論:| A. | ①②③④ | B. | ①②③ | C. | ①④ | D. | ②③ |
分析 連接CD根據等腰直角三角形的性質,就可以得出△ADE≌△CDF,根據全等三角形的性質得出AE=CF,進而得出CE=BF,就有AE+BF=AC,再由勾股定理就可以求出結論.
解答  解:如圖所示,連接CD,
解:如圖所示,連接CD,
∵AC=BC,點D為AB中點,∠ACB=90°,
∴AD=CD=BD=$\frac{1}{2}$AB,∠A=∠B=∠ACD=∠BCD=45°,∠ADC=∠BDC=90°,
∴∠ADE+∠EDC=90°,
∵∠EDC+∠FDC=∠GDH=90°,
∴∠ADE=CDF.
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠A=∠DCB}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△ADE≌△CDF(ASA),
∴AE=CF,DE=DF,S△ADE=S△CDF.
∵AC=BC,
∴AC-AE=BC-CF,
∴CE=BF.
∵AC=AE+CE,
∴AC=AE+BF.
∵AC2+BC2=AB2,AC=BC,
∴AC=$\frac{\sqrt{2}}{2}$AB,
∴AE+BF=$\frac{\sqrt{2}}{2}$AB,故①正確;
∵DE=DF,∠GDH=90°,
∴△DEF始終為等腰直角三角形,故②正確;
∵S四邊形CEDF=S△EDC+S△EDF,
∴S四邊形CEDF=S△EDC+S△ADE=$\frac{1}{2}$S△ABC,
又∵S△ABC=$\frac{1}{2}$AC2=$\frac{1}{2}$($\frac{\sqrt{2}}{2}$AB)2=$\frac{1}{4}$AB2,
∴S四邊形CEDF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{4}$AB2=$\frac{1}{8}$AB2,故③正確;
∵CE2+CF2=EF2,DE2+DF2=EF2,
∴CE2+AE2=EF2=DE2+DF2,
又∵DE=DF,
∴AE2+CE2=2DF2,故④正確;
∴正確的有①②③④.
故選A.
點評 本題考查了等腰直角三角形的性質,全等三角形的判定及性質,勾股定理以及三角形的面積公式的運用,根據ASA證明△ADE≌△CDF是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:A、B、C是一直線上順次三點,并且BC=90.
已知:A、B、C是一直線上順次三點,并且BC=90.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
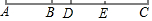 如圖,已知線段AB=3cm,延長線段AB到C,使BC=2AB.
如圖,已知線段AB=3cm,延長線段AB到C,使BC=2AB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$,$\frac{1}{16}$ | B. | $\frac{1}{2}$,$\frac{1}{8}$ | C. | $\frac{1}{4}$,$\frac{1}{8}$ | D. | $\frac{1}{2}$,$\frac{1}{16}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,點D在等邊△ABC邊CB的延長線上,點E是邊BC上的動點,連結AE,在AE的左側構造等邊△AEF,連結DF,若DB=2,則DF的最小值是$\sqrt{3}$.
如圖,點D在等邊△ABC邊CB的延長線上,點E是邊BC上的動點,連結AE,在AE的左側構造等邊△AEF,連結DF,若DB=2,則DF的最小值是$\sqrt{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com