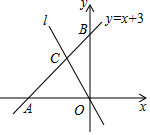Question

2．如圖，在平面直角坐標系中，已知直線y=x+3的圖象分別交x軸、y軸于A，B兩點，直線l經過原點與線段AB交于點C，且△AOC和△BOC的面積比是2：1．
（1）求A，B兩點的坐標；
（2）求直線l的解析式．

Answer 1

分析 （1）利用直線與坐標軸的交點解得A，B坐標；
（2）設直線l的解析式為y=kx，根據△AOC和△BOC的面積比是2：1，可得△AOC和△AOB的面積比是2：3，易得B，C的縱坐標比，可得C點的縱坐標，由直線y=x+3可得C點的橫坐標，可得直線l的解析式．

解答 解（1）令x=0，y=0+3=3，
∴B點坐標為（0，3）；
令y=0，可得0=x+3，
x=-3，
∴A點坐標為（-3，0）；

（2）∵S_△AOC：S_△BOC=2：1．
∴S_△AOC：S_△AOB=2：3；
∴B，C的縱坐標比為3：2，
∵B點的縱坐標為3，
∴C點的縱坐標為2，
∵點C在直線y=x+3上，
∴2=x+3，
∴x=-1，
∴點C的坐標為（-1，2），
∵直線l過原點，
∴設直線l的解析式為y=kx，把點C（-1，2）代入得k=-2．
∴直線l的解析式為y=-2x．

點評 本題主要考查了兩直線相交問題，掌握兩條直線的交點坐標，就是由這兩條直線相對應的一次函數表達式所組成的二元一次方程組的解是解答此題的關鍵．