
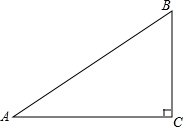
 如圖,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中點,點E在邊AC上,將△ADE沿DE翻折,使得點A落在點A'處,當A'E⊥AC時,A'B=$\sqrt{2}$或7$\sqrt{2}$.
如圖,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中點,點E在邊AC上,將△ADE沿DE翻折,使得點A落在點A'處,當A'E⊥AC時,A'B=$\sqrt{2}$或7$\sqrt{2}$. 分析 分兩種情況:
①如圖1,作輔助線,構建矩形,先由勾股定理求斜邊AB=10,由中點的定義求出AD和BD的長,證明四邊形HFGB是矩形,根據同角的三角函數列式可以求DG和DF的長,并由翻折的性質得:∠DA′E=∠A,A′D=AD=5,由矩形性質和勾股定理可以得出結論:A′B=$\sqrt{2}$;
②如圖2,作輔助線,構建矩形A′MNF,同理可以求出A′B的長.
解答 解:分兩種情況:
①如圖1,過D作DG⊥BC與G,交A′E與F,過B作BH⊥A′E與H,
∵D為AB的中點,
∴BD=$\frac{1}{2}$AB=AD,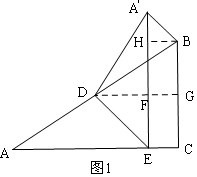
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC=$\frac{DG}{BD}=\frac{AC}{AB}$,
∴$\frac{DG}{5}=\frac{8}{10}$,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A=$\frac{BC}{AB}=\frac{DF}{A′D}$,
∴$\frac{6}{10}=\frac{DF}{5}$,
∴DF=3,
∴FG=4-3=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90°,
∴四邊形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=8-1=7,
∴A′H=A′E-EH=7-6=1,
在Rt△AHB中,由勾股定理得:A′B=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
②如圖2,過D作MN∥AC,交BC與于N,過A′作A′F∥AC,交BC的延長線于F,延長A′E交直線DN于M,
∵A′E⊥AC,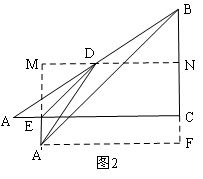
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四邊形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B=$\sqrt{{7}^{2}+{7}^{2}}$=7$\sqrt{2}$;
綜上所述,A′B的長為$\sqrt{2}$或7$\sqrt{2}$.
故答案為:$\sqrt{2}$或7$\sqrt{2}$.
點評 本題考查了翻折變換的性質、勾股定理、矩形的性質、三角函數及解直角三角形的有關知識,作輔助線構建矩形是本題的關鍵,明確翻折前后的對應角和邊相等,在證明中利用同角的三角函數列比例式比證明相似列比例式計算簡單.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:填空題
| 柑橘總質量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 損壞柑橘質量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘損壞的頻率$\frac{m}{n}$ (結果保留小數點后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 無解 | B. | 有一組解 | C. | 有無窮多解 | D. | 不確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com