Question

下列各函數中，y隨x的減小而減小的是（ ）
A．
B．
C．y=-x+1
D．y=2x-1

Answer 1

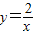
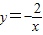
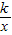【答案】分析：根據反比例函數y=（k≠0）的性質（k＜0時，該函數圖象經過第二、四象限，且在同一象限內y的值隨x值的增大而增大）、一次函數y=kx+b（k＞0時，y的值隨x值的增大而增大）解答．
解答：解：A、∵2＞0，
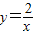∴函數的圖象在同一個象限內，y隨x的增大而減小；故本選項錯誤；
B、∵-2＜0，
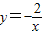∴函數的圖象在同一個象限內，y隨x的增大而增大，即y隨x的減小而減小；故本選項錯誤；
C、∵-1＜0，
∴一次函數y=-x+1的圖象在定義域內，y隨x的增大而減小；故本選項錯誤；
D、∵2＞0，
∴一次函數y=2x-1的圖象在定義域內，y隨x的增大而增大，亦或y隨x的減小而減小；故本選項正確．
故選D．
點評：本題考查了一次函數、反比例函數的性質．反比例函數的性質：①當k＞0時，圖象分別位于第一、三象限；當k＜0時，圖象分別位于第二、四象限．
②當k＞0時，在同一個象限內，y隨x的增大而減小；當k＜0時，在同一個象限，y隨x的增大而增大．