
分析 根據(jù)題意畫出圖形,∴△OAM是等邊三角形,易知M($\sqrt{3}$,1)或(-$\sqrt{3}$,1,利用待定系數(shù)法即可解決問題.
解答 解:如圖,∵AM=OM=OA=2,
∴△OAM是等邊三角形,
易知M($\sqrt{3}$,1)或(-$\sqrt{3}$,1)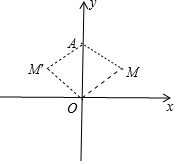
當(dāng)M($\sqrt{3}$,1)時,1=2$\sqrt{3}$+b,解得b=1-2$\sqrt{3}$,
當(dāng)M(-$\sqrt{3}$,1)時,1=-2$\sqrt{3}$+b,解得b=1+2$\sqrt{3}$,
故答案為:1-2$\sqrt{3}$或1+2$\sqrt{3}$.
點評 本題考查的是一次函數(shù)圖象上點的坐標(biāo)特點,熟知一次函數(shù)圖象上各點的坐標(biāo)一定適合此函數(shù)的解析式是解答此題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
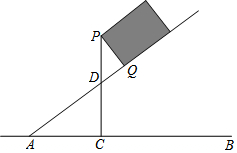 一長方形木箱沿斜面下滑,當(dāng)木箱滑至如圖所示位置時,AQ=m,己知木箱高PQ=h,斜面坡角α滿足tanα=$\frac{3}{4}$(α為銳角),求木箱頂端P離地面AB的距離PC.
一長方形木箱沿斜面下滑,當(dāng)木箱滑至如圖所示位置時,AQ=m,己知木箱高PQ=h,斜面坡角α滿足tanα=$\frac{3}{4}$(α為銳角),求木箱頂端P離地面AB的距離PC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 它與3πa2b是同類項 | B. | 它的系數(shù)是3 | ||
| C. | 它是二次單項式 | D. | 它與$-\frac{7}{2}{a^2}b$的和是2a2b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 不可能是負(fù)數(shù) | B. | 可能是零或者負(fù)數(shù) | ||
| C. | 必定是零 | D. | 必定是正數(shù) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
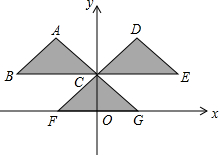 如圖,三角形CFG的頂點坐標(biāo)分別為C(0,$\frac{\sqrt{2}}{2}$),F(xiàn)(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移兩次,構(gòu)成如圖所示的圖案(其中點B、C、E在一條平行于x軸的直線上).
如圖,三角形CFG的頂點坐標(biāo)分別為C(0,$\frac{\sqrt{2}}{2}$),F(xiàn)(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移兩次,構(gòu)成如圖所示的圖案(其中點B、C、E在一條平行于x軸的直線上).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com