
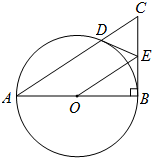
 如圖,以Rt△ABC的直角邊AB為直徑作⊙O與斜邊AC交于點D,E為BC邊的中點,連接DE,OE.
如圖,以Rt△ABC的直角邊AB為直徑作⊙O與斜邊AC交于點D,E為BC邊的中點,連接DE,OE.分析 (1)連接OD后,證明△DOE≌△BOE后,可得∠OBE=∠ODE=90°,所以DE是⊙O的切線;
(2)①由(1)可知:∠ODE=90°,要使四邊形AOED是平行四邊形,即需要DE∥AO,所以需要∠AOD=90°,又因為OA=OD,所以∠CAB=45°;
②由①可知:四邊形OBED是矩形,又因為OD=OB,所以四邊形OBED是正方形.
解答 解:(1)連接OD,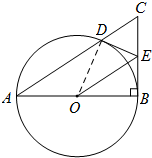 ∵E是BC的中點,
∵E是BC的中點,
O是AB的中點,
∴OE是△ABC的中位線,
∴OE∥AC,
∠BOE=∠BAC,
∠DOE=∠ADO,
∵OD=OA,
∴∠BAC=∠ADO,
∴∠BOE=∠DOE,
在△DOE與△BOE中,
$\left\{\begin{array}{l}{OD=OB}\\{∠DOE=∠BOE}\\{OE=OE}\end{array}\right.$,
∴△DOE≌△BOE,
∴∠OBE=∠ODE=90°,
∴DE是⊙O的切線;
(2)①當(dāng)∠CAB=45°時,
∴∠ADO=45°,
∴∠AOD=90°,
又∵∠EDO=90°,
∴DE∥AB,
∵OE∥AC,
∴四邊形AOED是平行四邊形;
②由①可知:∠EDO=∠DOB=∠ABC=90°,
∴四邊形OBED是矩形,
∵OD=OB,
∴矩形OBED是正方形.
故答案為:①45°;②正方形.
點評 本題考查圓的綜合問題,涉及全等三角形的判定與性質(zhì),切線的判定,平行四邊形的判定,正方形的判定等知識,考查學(xué)生靈活運(yùn)用知識的能力.


 高效智能課時作業(yè)系列答案
高效智能課時作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
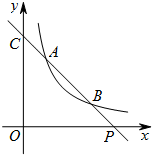 如圖,已知直線y=ax+b與雙曲線$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)兩點(A與B不重合),直線AB與x軸交于P(x0,0),與y軸交于點C.
如圖,已知直線y=ax+b與雙曲線$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)兩點(A與B不重合),直線AB與x軸交于P(x0,0),與y軸交于點C.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
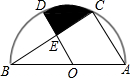 如圖,半圓O中,AB為直徑,AB=4,C、D為半圓上兩點,四邊形OACD為菱形,連接BC交OD于點E,則陰影部分面積為$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
如圖,半圓O中,AB為直徑,AB=4,C、D為半圓上兩點,四邊形OACD為菱形,連接BC交OD于點E,則陰影部分面積為$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com