
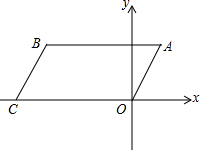
 如圖,四邊形ABCO是平行四邊形,點C在x軸的負半軸上,AO=2cm,AB=4cm,∠BAO=60°,將?ABCO繞點A逆時針旋轉60°,得到對應的?ADEF,解答下列問題:
如圖,四邊形ABCO是平行四邊形,點C在x軸的負半軸上,AO=2cm,AB=4cm,∠BAO=60°,將?ABCO繞點A逆時針旋轉60°,得到對應的?ADEF,解答下列問題:分析 (1)根據圖形旋轉的性質畫出旋轉后的?ADEF即可;
(2)過點A作AG⊥x軸于點G,根據銳角三角函數的定義得出OG與AG的長,再由∴?ABCO旋轉過程中掃過的區域的面積=S平行四邊形ABCO+S扇形ACE即可得出結論.
解答 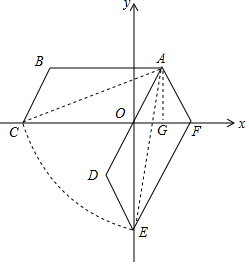 解:(1)如圖所示,?ADEF即為所求;
解:(1)如圖所示,?ADEF即為所求;
(2)過點A作AG⊥x軸于點G,
∵AB∥OC,∠BAO=60°,
∴∠AOG=60°,
∴OG=$\frac{1}{2}$AO=1,AG=AO•sin60°=$\sqrt{3}$,
∴S平行四邊形ABCO=AB•AG=4$\sqrt{3}$.
在Rt△ACG中,AC2=AG2+CG2=($\sqrt{3}$)2+(4+1)2=28,
∴S扇形ACE=$\frac{1}{6}$π×AC2=$\frac{14π}{3}$,
∴?ABCO旋轉過程中掃過的區域的面積=S平行四邊形ABCO+S扇形ACE=4$\sqrt{3}$+$\frac{14π}{3}$.
點評 本題考查的是作圖-旋轉變換,熟知圖形旋轉不變性的性質是解答此題的關鍵.


 作業輔導系列答案
作業輔導系列答案 同步學典一課多練系列答案
同步學典一課多練系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0.2! | B. | 2450 | C. | $\frac{25}{24}$ | D. | 49! |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,點P從原點O出發.沿x軸向右以每秒一個單位長的速度運動t秒(t>0),拋物線y=-x2+bx+c經過點O和點P.
如圖,在平面直角坐標系中,點P從原點O出發.沿x軸向右以每秒一個單位長的速度運動t秒(t>0),拋物線y=-x2+bx+c經過點O和點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
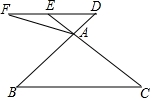 如圖,在△ABC中,點D是BA邊延長線上一點,過點D作DE∥BC,交CA延長線于點E,點F是DE延長線上一點,連接AF.
如圖,在△ABC中,點D是BA邊延長線上一點,過點D作DE∥BC,交CA延長線于點E,點F是DE延長線上一點,連接AF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
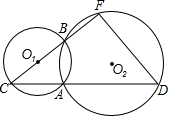 如圖,已知⊙O1與⊙O2交于A,B兩點,點C在⊙O1上且在⊙O2外,CA,CB的延長線分別與⊙O2交于點D,E,AC=3,AD=6,⊙O1的半徑為2.則點O1到DE的距離為 ( )
如圖,已知⊙O1與⊙O2交于A,B兩點,點C在⊙O1上且在⊙O2外,CA,CB的延長線分別與⊙O2交于點D,E,AC=3,AD=6,⊙O1的半徑為2.則點O1到DE的距離為 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com