
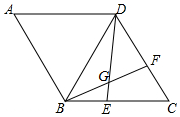
 如圖,在菱形ABCD中,AB=BD,點(diǎn)E,F(xiàn)分別在BC,CD邊上,且CE=DF,BF與DE交于點(diǎn)G,若BG=2,DG=4,則CD長為2$\sqrt{7}$.
如圖,在菱形ABCD中,AB=BD,點(diǎn)E,F(xiàn)分別在BC,CD邊上,且CE=DF,BF與DE交于點(diǎn)G,若BG=2,DG=4,則CD長為2$\sqrt{7}$. 分析 作輔助線,構(gòu)建全等三角形,證明△DBE≌△BCF和△BGD≌△BHC,計(jì)算DE=BF=$\frac{14}{3}$,再證明△BGE∽△BCF,列比例式得:$\frac{EG}{CF}=\frac{BE}{BF}$,求得CF=$±\frac{2\sqrt{7}}{3}$,從而得CD的長.
解答 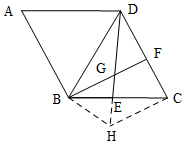 解:延長DE至H,使GH=BG,連接BH、CH,
解:延長DE至H,使GH=BG,連接BH、CH,
∵四邊形ABCD為菱形,
∴BC=DC=AB=BD,
∴△BDC是等邊三角形,
∴∠DBC=∠BCF=60°,
∵CE=DF,
∴BC-CE=CD-DF,
即BE=CF,
在△DBE和△BCF中,
∵$\left\{\begin{array}{l}{DB=BC}\\{∠DBC=∠BCF}\\{BE=CF}\end{array}\right.$,
∴△DBE≌△BCF(SAS),
∴∠BDG=∠FBC,
∴∠BDG+∠DBF=∠FBC+∠DBF=60°,
∴∠BGE=∠BDG+∠DBF=60°,
∴△BGH為等邊三角形,
∴BG=BH=2,∠GBH=60°,
∴∠DBF+∠FBC=∠HBC+∠FBC,
∴∠DBF=∠HBC,
在△BGD和△BHC中,
∵$\left\{\begin{array}{l}{BD=BC}\\{∠DBF=∠HBC}\\{BG=BH}\end{array}\right.$,
∴△BGD≌△BHC(SAS),
∴DG=CH=4,
∵∠FBC=∠BDG=∠BCH,
∴BF∥CH,
∴△BGE∽△CEH,
∴$\frac{BG}{CH}=\frac{EG}{EH}=\frac{BE}{CE}=\frac{2}{4}=\frac{1}{2}$,
∵EG+EH=2,
∴EG=$\frac{2}{3}$,
∴BF=DE=4+$\frac{2}{3}$=$\frac{14}{3}$,
∵∠FBC=∠FBC,∠BGE=∠BCD=60°,
∴△BGE∽△BCF,
∴$\frac{EG}{CF}=\frac{BE}{BF}$,
∴$\frac{\frac{2}{3}}{CF}$=$\frac{CF}{\frac{14}{3}}$,
∴CF2=$\frac{28}{9}$,
CF=$±\frac{2\sqrt{7}}{3}$,
∴BE=CF=$\frac{2\sqrt{7}}{3}$,
∴BC=3BE=3×$\frac{2\sqrt{7}}{3}$=2$\sqrt{7}$,
∴CD=BC=2$\sqrt{7}$.
故答案為:2$\sqrt{7}$.
點(diǎn)評(píng) 本題考查了菱形的性質(zhì)、三角形全等的性質(zhì)和判定、三角形相似的性質(zhì)和判定、等邊三角形的性質(zhì)和判定,作輔助線,構(gòu)建全等三角形是本題的關(guān)鍵,根據(jù)有一個(gè)角是60°的等腰三角形是等邊三角形得△BGH為等邊三角形是突破口.


 名師點(diǎn)睛字詞句段篇系列答案
名師點(diǎn)睛字詞句段篇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
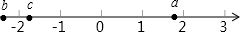 實(shí)數(shù)a、b、c在數(shù)軸上的對應(yīng)點(diǎn)如圖所示,其中|a|=|c|,化簡|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.
實(shí)數(shù)a、b、c在數(shù)軸上的對應(yīng)點(diǎn)如圖所示,其中|a|=|c|,化簡|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 圖象中所反應(yīng)的過程是:張強(qiáng)從家跑步去體育場,在那里鍛煉了一陣后,又去早餐店吃早餐,然后散步走回家,其中x表示時(shí)間,y表示張強(qiáng)離家的距離,根據(jù)圖象提供的信息,以下四個(gè)說法錯(cuò)誤的是( )
圖象中所反應(yīng)的過程是:張強(qiáng)從家跑步去體育場,在那里鍛煉了一陣后,又去早餐店吃早餐,然后散步走回家,其中x表示時(shí)間,y表示張強(qiáng)離家的距離,根據(jù)圖象提供的信息,以下四個(gè)說法錯(cuò)誤的是( )| A. | 體育場離張強(qiáng)家2.5千米 | |
| B. | 張強(qiáng)在體育場鍛煉了15分鐘 | |
| C. | 體育場離早餐店4千米 | |
| D. | 張強(qiáng)從早餐店回家的平均速度是$\frac{18}{7}$千米/小時(shí) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 32,28 | B. | 28,32 | C. | 28,28 | D. | 30,28 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2016-2017學(xué)年湖北省枝江市八年級(jí)3月調(diào)研考試數(shù)學(xué)試卷(解析版) 題型:單選題
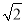 的倒數(shù)是( )
的倒數(shù)是( )
A. 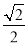 B.
B. 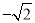 C.
C. 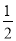 D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com