
| A. | 52012-1 | B. | 52013-1 | C. | $\frac{{5}^{2013}-1}{4}$ | D. | $\frac{{5}^{2012}-1}{4}$ |
分析 觀察題目中所給的推理方法:可以發現,當乘方的底數為2的時候,把原式乘上2,再與原式相減即可得出答案;因此當乘方中底數為5時,把原式乘上5,得到與原式類似的式子,再減去原式即可得到答案.據此解決.
解答 解:設S=1+5+52+53+…+52012,
則5S=5+52+53+54+…+52013,
所以5S-S=(5+52+53+54+…+52013)-(1+5+52+53+…+52012)
=5+52+53+54+…+52013-1-5-52-53-…-52012
=52013-1,
即4S=52013-1
所以S=$\frac{{5}^{2013}-1}{4}$;
故選:C.
點評 解決本題的關鍵是觀察題干中的推理過程,找到規律,然后應用規律解決問題.


科目:小學數學 來源: 題型:解答題
 媽媽的茶杯這樣放在桌子上(如圖).
媽媽的茶杯這樣放在桌子上(如圖).查看答案和解析>>
科目:小學數學 來源: 題型:解答題
查看答案和解析>>
科目:小學數學 來源: 題型:選擇題
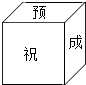 小亮為今年參加中考的好友小杰制作了一個正方體禮品盒(如圖),六個面上各有一個字,連起來就是“預祝中考成功”,其中“預”的對面是“中”,“成”的對面是“功”,則它的平面展開圖可能是( )
小亮為今年參加中考的好友小杰制作了一個正方體禮品盒(如圖),六個面上各有一個字,連起來就是“預祝中考成功”,其中“預”的對面是“中”,“成”的對面是“功”,則它的平面展開圖可能是( )| A. | 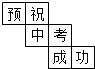 | B. | 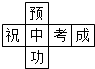 | C. |  | D. |  |
查看答案和解析>>
科目:小學數學 來源: 題型:解答題
查看答案和解析>>
科目:小學數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com