日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

13．(城西中學)已知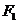、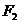是雙曲線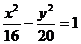的焦點，點P是雙曲線上一點，若P到焦點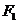的距離為9，則P到焦點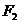的距離為___________.

正確答案：17

錯因：不注意取舍。

12．(城西中學)已知一條曲線上面的每一點到點A(0,2)的距離減去它到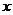軸的距離的差都是2,則這曲線的方程是_____________

正確答案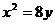：或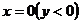

錯因：數形結合時考慮不全面。

11．(城西中學)已知F₁、F₂是橢圓　　　　　　　　 　的焦點，P是橢圓上一點，

且∠F₁PF₂=90°，

則橢圓的離心率e的取值范圍是　　　　　　　　　　 。

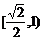
答案：　　　　　　

錯因：范圍問題主要是找不等關系式，如何尋求本題中的不等關系，忽視橢圓的范圍。

10．(磨中)過點M(-1，0)的直線l₁與拋物線y²=4x交于P₁，P₂兩點，記線段P₁P₂的中點為P，過P和這個拋物線的焦點F的直線為l₂，l₁的斜率為K，試把直線l₂的斜率與直線l₁的斜率之比表示為k的函數，其解析式為________，此函數定義域為________。

　 正確答案：f(k)=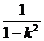　　 (-1，0)∪(0，1)

　 錯誤原因：忽視了直線l₁與拋物線相交于兩點的條件，得出錯誤的定義域。

9．(磨中)已知P是以F₁、F₂為焦點的雙曲線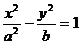上一點，PF₁⊥PF₂且tan∠PF₁F₂=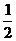，則此雙曲線的離心率為_______________。

　 正確答案：

　 　錯誤原因：忽視雙曲線定義的應用。

8．(磨中)雙曲線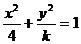的離心率為e，且e∈(1，2)則k的范圍是________。

　 正確答案：k∈(-12，0)

　 錯誤原因：混淆了雙曲線和橢圓的標準方程。

7．(磨中)過點(0，2)與拋物線y²=8x只有一個共點的直線有______條。

　 正確答案：3

　 錯誤原因：認為與拋物線只有一個共點的直線只能與拋物線相切而出錯。

6．(磨中)已知雙曲線的右準線為x=4，右焦點F(10，0)離心率e=2，則雙曲線方程為______。

　 正確答案：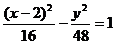

　 錯誤原因：誤認為雙曲線中心在原點，因此求出雙曲線的標準方程而出現錯誤。

5．(磨中)過點(3，-3)且與圓(x-1)²+y²=4相切的直線方程是：___________。

　 正確答案：5x+12y+21=0或x=3

　 錯誤原因：遺漏了斜率不存在的情形造成漏解。

4．(磨中)已知直線l₁：x+y-2=0　 l₂：7x-y+4=0 則l₁與l₂夾角的平分線方程為______。

　 正確答案：6x+2y-3=0

　 錯語原因：忽視兩直線夾角的概念多求了夾角的鄰補角的平分線方程。