
19.已知函數
1)若函數 在
在 處有極值
處有極值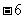 ,求
,求 的單調遞減區間;
的單調遞減區間;
2)若 的導數
的導數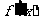 對
對 都有
都有 ,求
,求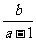 的取值范圍.
的取值范圍.
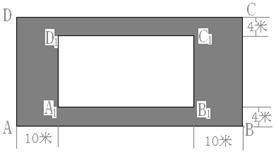
18.某房地產開發公司計劃在一樓區內建造一個長方形公園 ,公園由長方形的休閑區
,公園由長方形的休閑區
和環公園人行道(陰影部分)組成。已知休閑區 的面積為
的面積為 平方米,人行道的寬分別
平方米,人行道的寬分別
 為
為 米和
米和 米(如圖)(1)若設休閑區的長和寬的比
米(如圖)(1)若設休閑區的長和寬的比
 ,求公園
,求公園 所占面積
所占面積 關于
關于 的函數
的函數 的解析式;(2)要使公園所占面積最小,休閑區
的解析式;(2)要使公園所占面積最小,休閑區 的長和寬(長>寬)該如何設計?
的長和寬(長>寬)該如何設計?
⒖已知點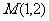 ,函數
,函數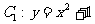 ,過點
,過點 作
作 的切線
的切線 ,
,
1)
求切線 的方程;
的方程;
2)
把函數 的圖象向下平移1個單位得到曲線
的圖象向下平移1個單位得到曲線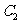 ,
,
求 與曲線
與曲線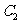 圍成圖形的面積.
圍成圖形的面積.
16.已知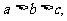
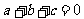 ,方程
,方程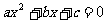 的兩個實數根為
的兩個實數根為 ,
,
1)求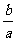 的取值范圍; 2)若
的取值范圍; 2)若 ,求
,求 的值. ( P104)
的值. ( P104)
⒘已知定義域為R的函數 是奇函數,其中
是奇函數,其中 是常數,且
是常數,且
1) 求 的值;
的值;
2)對任意的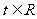 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
20、已知函數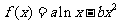 圖象上一點
圖象上一點 處的切線方程為
處的切線方程為
 . (Ⅰ)求
. (Ⅰ)求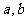 的值;
的值;
(Ⅱ)若方程 在
在 內有兩個不等實根,求
內有兩個不等實根,求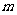 的取值范圍(其中
的取值范圍(其中 為自然對數的底數,
為自然對數的底數, );
);
(Ⅲ)令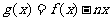 ,如果
,如果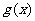 圖象與
圖象與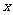 軸交于
軸交于 ,
, (
(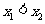 ),
), 中點為
中點為 ,求證:
,求證: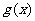 在
在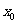 處的導數
處的導數 .
.
解:(Ⅰ) ,
, ,
,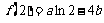 .
.
∴ ,且
,且 . …………………… 2分
. …………………… 2分
解得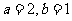 .
…………………… 3分
.
…………………… 3分
(Ⅱ) ,令
,令 ,
,
則 ,令
,令 ,得
,得 (
( 舍去).
舍去).
在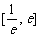 內,當
內,當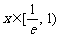 時,
時,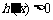 ,
∴
,
∴  是增函數;
是增函數;
當 時,
時,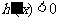 , ∴
, ∴  是減函數 …………………… 5分
是減函數 …………………… 5分
則方程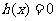 在
在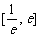 內有兩個不等實根的充要條件是
內有兩個不等實根的充要條件是 …………7分
…………7分
即 . …………………………… 8分
. …………………………… 8分
(Ⅲ)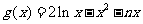 ,
, .
.
假設結論成立,則有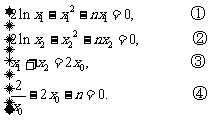 ………………………… 9分
………………………… 9分
①-②,得 .
.
∴ . …………………………………………………… 10分
. …………………………………………………… 10分
由④得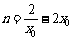 ,
,
∴ .即
.即 .
.
即 .⑤
…………………………………………………… 11分
.⑤
…………………………………………………… 11分
令 ,
, (
(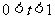 ), …………………………………… 12分
), …………………………………… 12分
則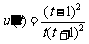 >0.∴
>0.∴ 在
在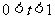 上增函數,
∴
上增函數,
∴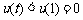 ,
……… 14分
,
……… 14分
∴⑤式不成立,與假設矛盾.
19、函數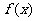 的定義域為
的定義域為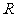 ,并滿足條件:① 對任意
,并滿足條件:① 對任意 ,有
,有 ;
;
② 對任意 ,有
,有 ;③
;③  .
.
(1)求 的值; (2)求證:
的值; (2)求證: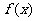 在
在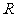 上是單調遞增函數;
上是單調遞增函數;
解:(1)令 ,則
,則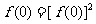

(2)任取 ,且
,且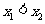
設 ,則
,則

 ,
,

 ,
,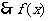 在
在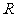 上是單調遞增函數
上是單調遞增函數
18、(14分)隨著機構改革工作的深入進行,各單位要減員增效,有一家公司現有職員
人(140< <420,且
<420,且 為偶數),每人每年可創利
為偶數),每人每年可創利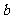 萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利
萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利 萬元,但公司需付下崗職員每人每年
萬元,但公司需付下崗職員每人每年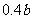 萬元的生活費,并且該公司正常運轉所需人數不得小于現有職員的
萬元的生活費,并且該公司正常運轉所需人數不得小于現有職員的 ,為獲得最大的年經濟效益,該公司應裁員多少人?
,為獲得最大的年經濟效益,該公司應裁員多少人?
解:設裁員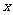 人,可獲得的經濟效益為
人,可獲得的經濟效益為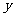 萬元,則
萬元,則
 =
=
依題意  ≥
≥ , ∴0<
, ∴0<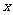 ≤
≤ .
.
又140< <420, 70<
<420, 70< <210.
<210.
① 當0< ≤
≤ ,即70<
,即70< ≤140時,
≤140時, ,
, 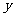 取到最大值;
取到最大值;
② 當 >
> ,即140<
,即140< <210時,
<210時, ,
, 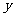 取到最大值;
取到最大值;
答:當70< ≤140時,應裁員
≤140時,應裁員 人;當140<
人;當140< <210時,應裁員
<210時,應裁員 人.
人.
17、(14分)已知函數f(x)=2x3+ax2+bx+3在x=-1和x=2處取得極值.
(1)求f(x)的表達式和極值.
(2)若f(x)在區間[m,m+4]上是單調函數,試求m的取值范圍.
解:(1)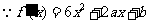
由已知有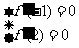 ,即
,即

 解得
解得

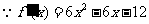
由 解得
解得 
由 解得
解得 
故函數f(x)在 和
和 是增函數,在
是增函數,在 上是減函數;
上是減函數;
當 時,有極大值10 , 當
時,有極大值10 , 當 時,有極小值
時,有極小值
(2)由(1)可知,要使f(x)在區間[m,m+4]上是單調函數時,須
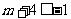 或
或  或
或

16、(12分)已知 ,設命題
,設命題 函數
函數 在
在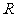 上單調遞增,命題
上單調遞增,命題 不等式
不等式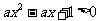 對
對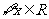 恒成立。若“
恒成立。若“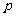 且
且 ”為假,“
”為假,“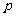 或
或 ”為真,求
”為真,求 的取值范圍。
的取值范圍。
解:由函數 在
在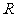 上單調遞增,可得
上單調遞增,可得
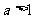
再由不等式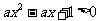 對
對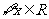 恒成立,可得
恒成立,可得


由于“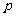 且
且 ”為假,“
”為假,“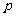 或
或 ”為真,故有
”為真,故有
 或
或


15、(12分)已知集合 ,
, ,若
,若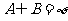 ,求實
,求實
數 的取值范圍。
的取值范圍。
解:
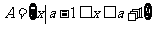 ,
,
又
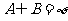 ,故有
,故有

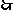
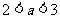
14、 3
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com