日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

1.排列與組合

⑴ 分類計數原理與分步計數原理是關于計數的兩個基本原理，兩者的區別在于分步計數原理和分步有關，分類計數原理與分類有關.

⑵ 排列與組合主要研究從一些不同元素中，任取部分或全部元素進行排列或組合，求共有多少種方法的問題.區別排列問題與組合問題要看是否與順序有關，與順序有關的屬于排列問題，與順序無關的屬于組合問題.

⑶ 排列與組合的主要公式

①排列數公式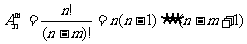： (m≤n)　

A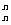=n! =n(n―1)(n―2) ·…·2·1.

②組合數公式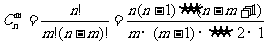：　(m≤n).

③組合數性質：①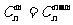(m≤n).　　　　 ②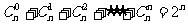　 　　

③

10．某初級中學有學生270人，其中一年級108人，二、三年級各81人，現要利用抽樣方法抽取10人參加某項調查，考慮選用簡單隨機抽樣、分層抽樣和系統抽樣三種方案，使用簡單隨機抽樣和分層抽樣時，將學生按一、二、三年級依次統一編號為1，2，…，270；使用系統抽樣時，將學生統一隨機編號為1，2，…，270，并將整個編號依次分為10段.如果抽得號碼有下列四種情況：

　　　 ①7，34，61，88，115，142，169，196，223，250；

　　　 ②5，9，100，107，111，121，180，195，200，265；

　　　 ③11，38，65，92，119，146，173，200，227，254；

　　　 ④30，57，84，111，138，165，192，219，246，270；

　　　 關于上述樣本的下列結論中，正確的是

　　　 A．②、③都不能為系統抽樣　　 　　　　　　　　　　 B．②、④都不能為分層抽樣

　 C．①、④都可能為系統抽樣　　 　　　　　　　　　　 D．①、③都可能為分層抽樣

9．從5名男生、1名女生中，隨機抽取3人，檢查他們的英語口語水平，在整個抽樣過程中，若這名女生第一次、第二次均未被抽到，那么她第三次被抽到的概率是

A．　　　 　　　　　　　 B．　　　　 　　　　　　　　 C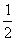．　　　　 　　　　　　 D．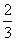

8．對一組數據x_i(i＝1，2，…，n)，如將它們改為x_i－m(i＝1，2，…，n)，其中m≠0．則下面結論正確的是

A．平均數與方差都不變　　　　 　　　　　　　　　 B．平均數與方差都變了

C．平均數不變，方差變了　　　　　　　　　　　　　　　 D．平均數變了，方差不變

7．如圖所示是一批產品中抽樣得到數據的頻率直方圖，

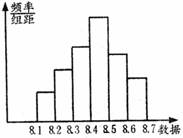　 由圖可看出概率最大時數據所在范圍是

　　　 A．(8.1，8.3)

　　　 B．(8.2，8.4)

　　　 C．(8.4，8.5)

D．(8.5，8.7)

6．某公司在甲、乙、丙、丁四個地區分別有150個、120個、180個、150個銷售點.公司為了調查產品銷售的情況，需從這600個銷售點中抽取一個容量為100的樣本，記這項調查為①；在丙地區中有20個特大型銷焦點，要從中抽取7個調查其銷售收入和售后服務情況，記這項調查為②．則完成①、②這兩項調查宜采用的抽樣方法依次是

　 A．分層抽樣，系統抽樣法 　　　　　　　　　　　　　　 B．分層抽樣法，簡單隨機抽樣法

C．系統抽樣法，分層抽樣法　 　　　　　　　　　　　 D．簡隨機抽樣法，分層抽樣法

5．為了了解全校1320名高一學生的身高情況，從中抽取220名學生進行測量，下列說法正確的是

　 　A．樣本容量是220　　　 　　　　　　　　　　　　　　　　 B．個體是每一個學生

C．樣本是220名學生　　　　　 　　　　　　　　　　 D．總體是1320

4．若m個數的平均數是x，n個數的平均數是y，則這m+n個數的平均數是

A．　 　　　　　　　 B．　 　　　　　　 C． 　　　　 D．

3．某工廠生產A、B、C三種不同型號的產品，產品數量之比依次為2:3:5，現用分層抽樣方法抽出一個容量為n的樣本，樣本中A種型號產品有16件．那么此樣本的容量n＝

A．60 　　　　　　　　　　　　　 B．70 　　　　　　　　　　　　 C．80　　　　　　　　　 D．90

2．已知10個數據：

1203　 1201　 1194　 1200　 1204　 1201　 1199　 1204　 1195　 1199

它們的平均數是

A．1400　 　　　B．1300　 　　C．1200　 　D．1100