
g(x)∈M,∴存在區間[a,b]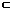 [1,+∞],滿足g(a)=a,g(b)=b.
[1,+∞],滿足g(a)=a,g(b)=b.
即方程g(x)=x在[1,+∞]內有兩個不等實根.
[法一]:方程+t=x在[1,+∞]內有兩個不等實根,等價于方程x-1=(x-t)2在[2t,+∞]內有兩個不等實根.
即方程x2-(4t+4)x+4t2+4=0在[2t,+∞]內有兩個不等實根.
22. (本小題滿分12分)已知集合M是同時滿足下列兩個性質的函數f(x)的全體:①f(x)在其定義域上是單調增函數或單調減函數;②在f(x)的定義域內存在區間[a,b],使得f(x)在[a,b]上的值域是[a,b].(1)判斷函數y=-x3是否屬于集合M?并說明理由.若是,請找出區間[a,b].(2)若函數y=+t∈M,求實數t的取值范圍.
解:(1)y=-x3的定義域是R,
y'=-3x2≤0,∴y=-x3在R上是單調減函數.
則y=-x3在[a,b]上的值域是[-b3,-a3].
由 解得:或 (舍去)或 (舍去)
∴函數y=-x3屬于集合M,且這個區間是[-,]??????????? 6分
(2)設g(x)=+t,則易知g(x)是定義域[1,+∞]上的增函數.
∴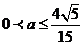 。?????????????????????????? 12分
。?????????????????????????? 12分
故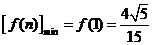
∴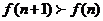 ,即
,即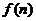 遞增,
遞增,
則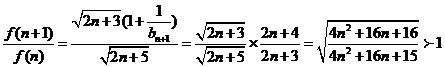
記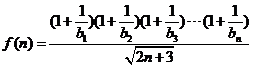
⑵
同理,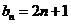 ???????????????????????? 4分
???????????????????????? 4分
解:⑴由已知得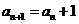 ,∴
,∴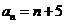
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com