
題目列表(包括答案和解析)
如圖1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通過以下計算:由題意,∠B=30°,∠C=90°,c=2b,a=![]() b,得a2-b2=(
b,得a2-b2=(![]() b)2-b2=2b2=b?c.即a2-b2= bc.
b)2-b2=2b2=b?c.即a2-b2= bc.
于是,小明猜測:對于任意的ΔABC,當∠A=2∠B時,關系式a2-b2=bc都成立.
(1)如圖2,請你用以上小明的方法,對等腰直角三角形進行驗證,判斷小明的猜測是否正確,并寫出驗證過程;
(2)如圖3,你認為小明的猜想是否正確,若認為正確,請你證明;否則,請說明理由;
(3)若一個三角形的三邊長恰為三個連續偶數,且∠A=2∠B,請直接寫出這個三角形三邊的長,不必說明理由.
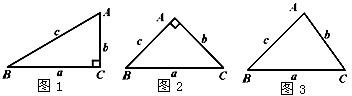
如下圖(1),由直角三角形邊角關系,可將三角形面積公式變形,
得 ![]() =
=![]() bc?sin∠A. ①
bc?sin∠A. ①
即三角形的面積等于兩邊之長與夾角正弦之積的一半.
如下圖(2),在ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ ![]() , 由公式①,得
, 由公式①,得
![]() AC?BC?sin(α+β)=
AC?BC?sin(α+β)= ![]() AC?CD?sinα+
AC?CD?sinα+![]() BC?CD?sinβ,
BC?CD?sinβ,
即 AC?BC?sin(α+β)= AC?CD?sinα+BC?CD?sinβ. ②
你能利用直角三角形邊角關系,消去②中的AC、BC、CD嗎?不能,說明理由;能,寫出解決過程.
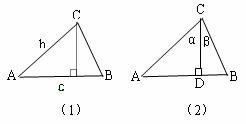
如圖1,線段![]() 過圓心O,交圓O于A,B兩點,PC切圓O于點C,作
過圓心O,交圓O于A,B兩點,PC切圓O于點C,作![]() ,垂足為D,連結AC,BC。
,垂足為D,連結AC,BC。
(1)寫出圖1中所有相等的角(直角除外),并給出證明;
(2)若圖1中的切線PC變為圖2中割線PCE的情形,PCE與圓O交于C,E兩點,AE與BC交于點M,![]() ,寫出圖2中相等的角(寫出三組即可,直角除外);
,寫出圖2中相等的角(寫出三組即可,直角除外);
(3)在圖2中,證明:AD?AB=AC?AE。


我國東南沿海某地的風力資源豐富,一年內日平均風速不小于3米/秒的時間共約160天,其中日平均風速不小于6米/秒的時間約占60天。
為了充分利用“風能”這種“綠色能源”,該地擬建一個小型風力發電場,決定選用A、B兩種型號的風力發電機。根據產品說明,這兩種風力發電機在各種風速下的日發電量(即一天的發電量)如下表:
| 日平均風速 |
| 3≤ |
| |
| 日發電量(千瓦?時) | A型發電機 | 0 | ≥36 | ≥150 |
| B型發電機 | 0 | ≥24 | ≥90 | |
根據上面的數據回答:
(1)若這個發電場購![]() 臺A型風力發電機,則預計這些A型風力發電機一年的發電總量至少為_____________千瓦?時;
臺A型風力發電機,則預計這些A型風力發電機一年的發電總量至少為_____________千瓦?時;
(2)已知A型風力發電機每臺0.3萬元,B型風力發電機每臺0.2萬元,該發電機擬購置風力發電機共10臺,希望購機的費用不超過2.6萬元,而建成的風力發電場每年的發電總量不少于102000千瓦?時,請你提供符合條件的購機方案。
如圖1,草原上有A,B,C三個互通公路的奶牛養殖基地,B與C之間距離為100千米,C在B的正北方,A在C的南偏東47°方向且在B的北偏東43°方向.A地每年產奶3萬噸;B地有奶牛9 000頭,平均每頭牛的年產奶量為3噸;C地養了三種奶牛,其中黑白花牛的頭數占20%,三河牛的頭數占35%,其他情況反映在圖2,圖3中.
(1)通過計算補全圖3;
(2)比較B地與C地中,哪一地平均每頭牛的年產奶量更高?
(3)如果從B,C兩地中選擇一處建設一座工廠解決三個基地的牛奶加工問題,當運送一噸牛奶每千米的費用都為1元(即1元/噸?千米時,那么從節省運費的角度考慮,應在何處建設工廠?

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com