
2005/2006�W(xu��)��Ƚ��K�}���и����ڶ����{(di��o)�п�ԇ
��(sh��) �W(xu��) ԇ �}
�ڢ��(�x���} ��60��)
 һ���x���}: �����}��12С�}��ÿС�}5�֣���60��.��ÿС�}�o�����Ă��x�(xi��ng)�У�ֻ��һ���Ƿ����}ĿҪ���.
һ���x���}: �����}��12С�}��ÿС�}5�֣���60��.��ÿС�}�o�����Ă��x�(xi��ng)�У�ֻ��һ���Ƿ����}ĿҪ���.
1.�O(sh��)ȫ��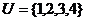 �ɂ�����
�ɂ�����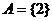 ��
��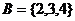 ���t
����
���t
����
A. {1} B. {1��3��4} C. {2} D. {3��4}
2. ��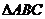 ��,
��,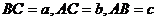 ,���
,���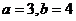 ,��ô��
,��ô��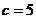 ���ǡ�
���ǡ�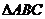 ��ֱ�������Ρ���
��ֱ�������Ρ���
A.��ֲ���Ҫ�l�� B.��Ҫ����֗l��
C. ��Ҫ�l�� D.�Ȳ��dz���ֲ��DZ�Ҫ�l��
3. ��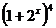 ��չ�_ʽ�ĵ�3�(xi��ng)��12���tx����
��չ�_ʽ�ĵ�3�(xi��ng)��12���tx����
A.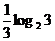 B.
B.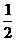 C.
C.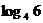 D.2
D.2
4.���タ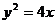 ���c(di��n)
���c(di��n)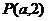 �����c(di��n)F�ľ��x��
�����c(di��n)F�ľ��x��
A. 1 B.
5.��֪��(sh��)��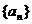 ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��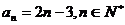 ����ǰn�(xi��ng)�͞�
����ǰn�(xi��ng)�͞�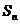 ���tʹ
���tʹ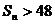 ������n����Сֵ��
������n����Сֵ��
A .7 B.
6. ����(sh��)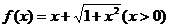 �ķ�����(sh��)��
�ķ�����(sh��)��
A.  B.
B.
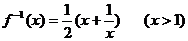
C. 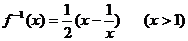 D.
D.
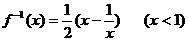
7. ��֪����(sh��)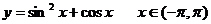 ���t�������_����
���t�������_����
A. ��ż����(sh��)�������ֵ��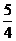 B. ��ż����(sh��)������Сֵ��
B. ��ż����(sh��)������Сֵ��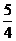
C. ��ż����(sh��)�������ֵ��2 D. ���溯��(sh��)���]����Сֵ
8. �O(sh��)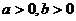 ���t���²���ʽ�в����������
���t���²���ʽ�в����������
A. 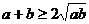 B.
B. 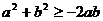
C. 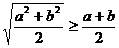 D.
D. 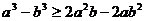
9. ���x��y�M��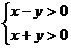 ���t��
���t��
A. 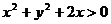 B.
B.
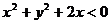
C. 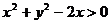 D.
D.
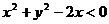
10. ��֪����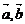 �ǃɂ��������ķ�������, ����
�ǃɂ��������ķ�������, ����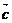 �M��
�M��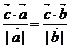 .�t����
.�t����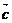 ������
������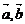 һ�����Ա�ʾ��
һ�����Ա�ʾ��
A. 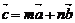 ��
��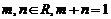 . B.
. B. 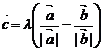
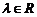
C. 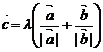
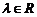
D. 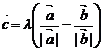
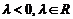 , ��
, �� 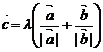
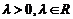
��������}:�����}��4С�}��tÿС�}4�ֹ�16��.
13.����(sh��)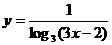 �Ķ��x����
.
�Ķ��x����
.
14.��֪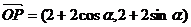 ��
��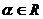 ����O������(bi��o)ԭ�c(di��n)��������
����O������(bi��o)ԭ�c(di��n)��������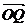 �M��
�M��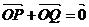 ���t���c(di��n)Q��܉�E������
.
���t���c(di��n)Q��܉�E������
.
15.������10�˵�һ����(sh��)�W(xu��)С�M��һ�Δ�(sh��)�W(xu��)�y�(y��n)���yԇ�}��10�����(xi��ng)�x���}��(g��u)�ɣ�ÿ����1�}��5�֣����e���0�֣���醺�Ľy(t��ng)Ӌ(j��)�÷���r����
�÷�
50��
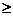 45��
45��
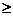 40��
40��
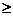 35��
35��
�˔�(sh��)
2
4
8
10
�t�@�Μyԇ��ƽ���ɿ�?y��u)?u> .
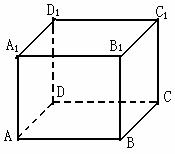 16.����������
16.����������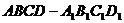 �У������߅������ABCD��߅�L
�У������߅������ABCD��߅�L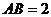 ����(c��)��
����(c��)��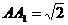 ���t���������}��
���t���������}��
��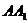 �c
�c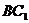 ��
��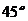 �ǣ�
�ǣ�
�� 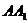 �c
�c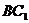 �ľ��x��2 ��
�ľ��x��2 ��
�� �����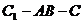 ��
�� ��
��
�� 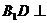 ƽ��
ƽ��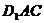 .
.
�t���_���}����̖�� .
17����֪�ɂ�����(sh��)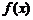 ��
��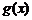 �Ķ��x���ֵ���Ǽ���{1,2,3},�䶨�x���±�.
�Ķ��x���ֵ���Ǽ���{1,2,3},�䶨�x���±�.
x
1
2
3
f��x��
2
3
1
x
1
2
3
g��x��
1
3
2
�����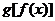 �ı���
�ı���
x
1
2
3
g (f��x��)
18���F(xi��n)Ҫ�o�����F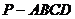 ���傀��Ϳ���ɫ��Ҫ����������Ϳ��ͬ���ɫ���ɹ��x����ɫ����4�N���t��ͬ��Ϳɫ�����ķN��(sh��)����
�N��
���傀��Ϳ���ɫ��Ҫ����������Ϳ��ͬ���ɫ���ɹ��x����ɫ����4�N���t��ͬ��Ϳɫ�����ķN��(sh��)����
�N��
��������}:�����}��5С�}����70��.���(y��ng)���������f����x�C���^�̻����㲽�E.
17��( ���}�M��12��)
�S�N��Ⱥ�и��NѪ�͵�����ռ�ı����±���ʾ��
Ѫ��
A
B
AB
O
ԓѪ�͵�����ռ/%
28
29
8
35
��֪ͬ�NѪ�͵��˿���ݔѪ��O��Ѫ����ݔ�o��һ�NѪ�͵Ă��ˣ��κ��˵�Ѫ������ݔ�oAB�͵��ˣ�������ͬѪ�͵��˲��ܻ���ݔѪ.С����B��Ѫ����С����ҪݔѪ������
(1)����һ����,��Ѫ����ݔ�oС���ĸ����Ƕ��٣�
(2)���҃ɂ��ˣ���(d��ng)��������һ���ˣ���Ѫ����ݔ�oС���ĸ����Ƕ��٣�
18. ( ���}�M��14��)
 ��D�������F
��D�������F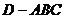 ��
�У�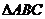 ��߅�L��4���������Σ�
��߅�L��4���������Σ�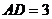 ��E��AB�����c(di��n)��
��E��AB�����c(di��n)�� .
.
(1) ���C��ƽ��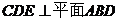 ;
;
(2) ��ֱ�� ��ƽ��CDE���ɵĽǵĴ�С��
��ƽ��CDE���ɵĽǵĴ�С��
(3) ���c(di��n)A��ƽ��BCD�ľ��x.
19. ( ���}�M��14��)
��֪����(sh��)��(sh��)��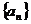 �У�
��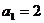 .���P(gu��n)��
.���P(gu��n)��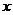 �ķ���
�ķ���
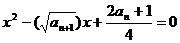
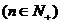 ����ȵČ�(sh��)��.
����ȵČ�(sh��)��.
(1)��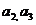 ��ֵ;
��ֵ;
��2�����C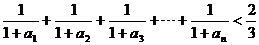
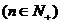 .
.
20. ( ���}�M��15��)
��֪�p����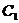 �ķ��̞�
�ķ��̞�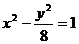 ���E�A
���E�A �L�S�ăɂ����c(di��n)ǡ�Þ��p����
�L�S�ăɂ����c(di��n)ǡ�Þ��p����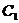 �ăɂ����c(di��n).
�ăɂ����c(di��n).
��1������E�A �ăɂ����c(di��n)�����p�����ăɂ���c(di��n)����E�A
�ăɂ����c(di��n)�����p�����ăɂ���c(di��n)����E�A �ķ���;
�ķ���;
��2������E�A �ķ��̞�
�ķ��̞� ���ҙE�A
���ҙE�A �ϴ��ڃ��c(di��n)A��B�P(gu��n)��ֱ��
�ϴ��ڃ��c(di��n)A��B�P(gu��n)��ֱ��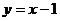 ���Q����
���Q����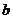 ȡֵ����.
ȡֵ����.
21.( ���}�M��15��)
��֪����(sh��)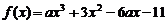 ,
,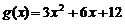 ,��ֱ��m��
,��ֱ��m��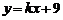 .��
.��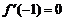 .
.
(1)��a��ֵ��
(2)�Ƿ����k��ֵ��ʹֱ��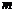 ��������y=f��x�����о�������y=g(x)
���о���������ڣ����k��ֵ�����������,�f������.
��������y=f��x�����������y=g(x)
���о���������ڣ����k��ֵ�����������,�f������.
(3)�����������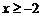 ��x,����
��x,����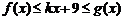 ��������k��ȡֵ����.
��������k��ȡֵ����.
�}����2005/2006�W(xu��)��ȸ����ڶ����{(di��o)�п�ԇ
tx��(sh��) �W(xu��) ԇ �� �� ��
1.D 2.A 3.B 4.B 5.C 6.C 7.A 8.D 9. A 10.C
11. 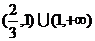 12.
12. 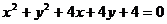 13. 42 14. �ڢ� 15.3,2,1 16.72
13. 42 14. �ڢ� 15.3,2,1 16.72
18. (1)������һ���ˣ���Ѫ�͞�A��B��AB��O�͵��¼��քeӛ��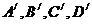 �������ǻ���ģ�����֪����
�������ǻ���ģ�����֪����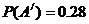 ��
��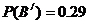
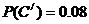
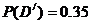
��?y��n)�B��O��Ѫ����ݔ�oB��Ѫ���ˣ��ʡ�����ݔ�oB��Ѫ���ˡ����¼�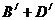
����(j��)�����¼��ļӷ���ʽ����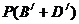 =
=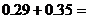
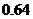 .
.
�����κ�һ��.��Ѫ����ݔ�oС���ĸ���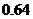
(2) ����A��AB��Ѫ����ݔ�oB��Ѫ���ˣ�һ���ˡ�����ݔ�oB�͵��ˡ����¼�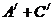
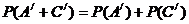 =
=
���κɂ��ˣ�����������һ���ˣ�����ݔ�oС�������¼�ӛ��E�����Č����¼��飺�ɂ��˶�����ݔѪ�oС�����t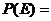
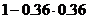 =
=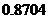 .
.
���ԣ��κζ����ˣ�����������һ���ˣ���Ѫ����ݔ�oС���ĸ��ʞ�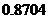
����
19. (1) 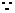
 ��
��

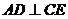 ����
����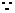
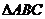 ����������E��AB�����c(di��n)��
����������E��AB�����c(di��n)��
 ��
��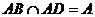

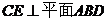 ����
����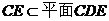

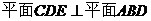
��2���ɣ�1����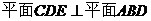 ��
�� AD��ƽ��CDE�ϵ���Ӱ��DE
AD��ƽ��CDE�ϵ���Ӱ��DE
����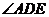 �������ɵĽ�.
�������ɵĽ�.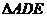 ��
��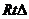 ����AE=2��AD=3��
����AE=2��AD=3��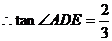

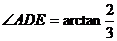 ����ֱ��AD�cƽ��CDE���ɵĽǞ�
����ֱ��AD�cƽ��CDE���ɵĽǞ�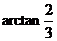
��3��ȡBC�����c(di��n)M���B��DM���^A�c(di��n)��ƽ��DAM��(n��i)��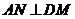 ��N
��N
�C��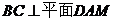 ������
������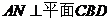
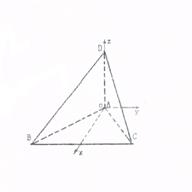 AM=
AM=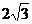 ��DM=
��DM=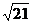 ��
��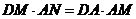 ����
����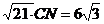
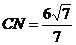
������2����10������Ҋֱ������(bi��o)ϵ����D��
��E��AB�����c(di��n)����E�c(di��n)����(bi��o)�飨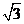 ��-3��0����
��-3��0����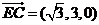
�O(sh��)ƽ��CDE�ķ�����m=��s,t,1��
�t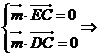
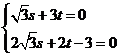 ��
��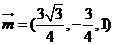
��ƽ��ABD�ķ�������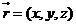 ��
��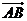 =��
=��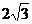 ��-2��0��
��-2��0�� 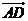 =��0��0��3��
=��0��0��3��
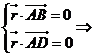
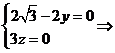
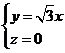 �����O(sh��)x=1���t
�����O(sh��)x=1���t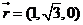
��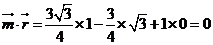 ��
��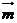 ��
�� ��ƽ��CDE��ƽ��ABD
��ƽ��CDE��ƽ��ABD
��2���O(sh��)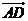 �c
�c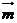 �ĊA�Ǟ�
�ĊA�Ǟ�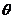 ���tcos
���tcos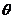 =
=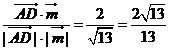
��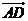 �c
�c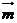 �ĊA�Ǟ�arccos
�ĊA�Ǟ�arccos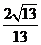 ��AD�cƽ��CDE���ɵĽǞ�
��AD�cƽ��CDE���ɵĽǞ�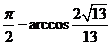
��3���t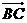 =��0��4��0����
=��0��4��0���� =��2
=��2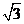 ��2��-3����
��2��-3����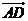 =��0��0��3���O(sh��)ƽ��BCD�ķ�������
=��0��0��3���O(sh��)ƽ��BCD�ķ�������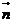 =��p,q,1��
=��p,q,1��
�t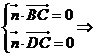

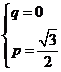 �t
�t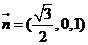
����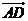 =��0��0��3����
=��0��0��3����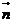 =��
=�� ��0��1���ϵ�ͶӰ��
��0��1���ϵ�ͶӰ��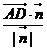 =
=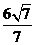
20.�⣺(1)���}��� ��
�� ��
��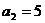 ��
��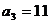
��2������ =
=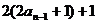 =
=
=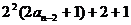 =
=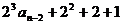 =
=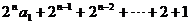 =
=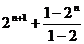 =
=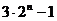

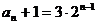
��an+1=2an+1 ��an+1+1=2(an+1) ��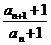 =2 ��a1+1=2+1=3 ��an+1=3?2n-1
=2 ��a1+1=2+1=3 ��an+1=3?2n-1
�t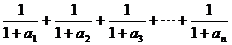 =
=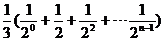
=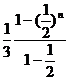 =
=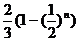
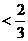 ����
����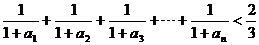
21.�⣨1�����p����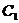 �ķ���
�ķ���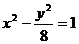 ��
��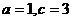 ���t�E�A
���t�E�A ���̞�
���̞�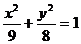
��2���E�A ���̞�
���̞�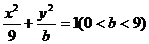 �� A��B�c(di��n)����ֱ�������O(sh��)��
�� A��B�c(di��n)����ֱ�������O(sh��)��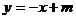 ��
��
����E�A ���̵�
���̵�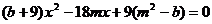
��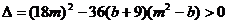 ��
��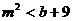 �O(sh��)
�O(sh��)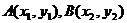 ��ô
��ô
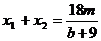 ��
�� 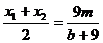 ������
������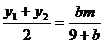
��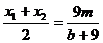 ��
��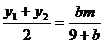
����ֱ��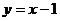 ��
�� �ٌ�
�ٌ� ����
����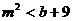 ��
��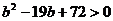 ��
��
���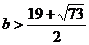 ����ȥ����
����ȥ����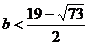 ��
��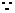
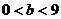

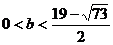
22.�⣺��1����?y��n)?sub>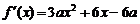 ,����
,����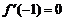 ��
��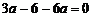 ,����a=��2.
,����a=��2.
(2)��?y��n)�ֱ��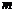 ���^�c(di��n)��0��9��.
���^�c(di��n)��0��9��.
����ֱ��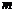 ��y=g(x)
���о�.�O(sh��)���c(di��n)��
��y=g(x)
���о�.�O(sh��)���c(di��n)��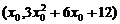 ,��?y��n)?sub>
,��?y��n)?sub>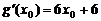 .
.
�����о����̞�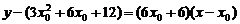 ,���c(di��n)��0��9�������
,���c(di��n)��0��9�������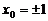 .
.
��(d��ng) �r���о����̞�y=9,
��(d��ng)
�r���о����̞�y=9,
��(d��ng)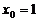 �r���о����̞�y=12x+9.
�r���о����̞�y=12x+9.
��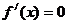 ��
��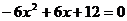 ������
������
��(d��ng)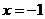 �r��
�r��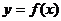 ���о�
���о�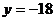 ��
��
��(d��ng)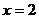 �r��
�r�� 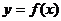 ���о����̞�
���о����̞�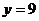

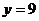 �ǹ��о���
�ǹ��о���
����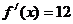 ��
��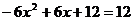

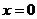 ��
��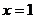 ��
��
��(d��ng)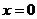 �r
�r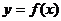 �����
�����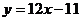 ��
��
��(d��ng)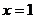 �r
�r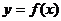 �����
�����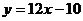 ��
��
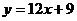 �����ǹ��о�
�����ǹ��о�
�C������ 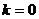 �r
�r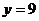 �ǃ������Ĺ��о�
�ǃ������Ĺ��о�
(3).��1��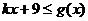 ��
��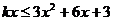 ����(d��ng)
����(d��ng)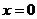 ������ʽ�������
������ʽ�������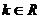 .
.
��(d��ng)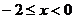 �r������ʽ��
�r������ʽ��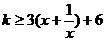 ��
��
��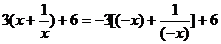
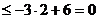
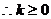
��(d��ng)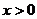 �r������ʽ��
�r������ʽ��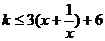 ��
��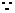
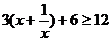

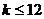
 ��(d��ng)
��(d��ng)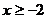 �r,
�r,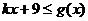 ��������t
��������t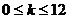
��2����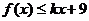 ��
��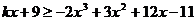
��(d��ng)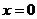 �r��
�r��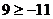 �������
�������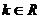 ����(d��ng)
����(d��ng)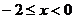 �r��
�r��
�O(sh��)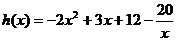 =
=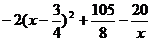 ��
��
��(d��ng)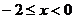 �r
�r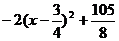 ��������(sh��)��
��������(sh��)��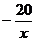 Ҳ��������(sh��)
Ҳ��������(sh��)

 Ҫʹ
Ҫʹ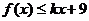 ��
��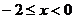 �Ϻ�������t
�Ϻ�������t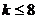
�������^��ֻҪ���]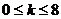 ���t��(d��ng)
���t��(d��ng)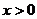 �r
�r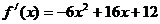 =
=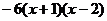
 ��
��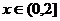 �r
�r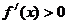 ����
����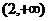 �r
�r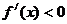

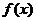 ��
��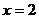 �r�ИO��ֵ��
�r�ИO��ֵ��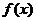 ��
��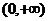 �ϵ����ֵ����
�ϵ����ֵ����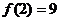 ����
����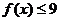 ����(d��ng)
����(d��ng)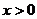 ,
,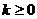 �r
�r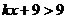 ��
��
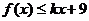 һ������
һ������
�C������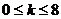 .
.
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com