日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】將一顆均勻的骰子擲兩次，第一次得到的點數記為，第一次得到的點數記為，則方程組有唯一解的概率是___________．

【題目】若函數滿足:對于任意正數，都有，且，則稱函數為“L函數”．

（1）試判斷函數與是否是“L函數”；

（2）若函數為“L函數”，求實數a的取值范圍；

（3）若函數為“L函數”，且，求證：對任意，都有．

【題目】設F1、F2分別為橢圓C：＝1（a＞b＞0）的左、右焦點，點A為橢圓C的左頂點，點B為橢圓C的上頂點，且|AB|＝，△BF1F2為直角三角形．

（1）求橢圓C的方程；

（2）設直線y＝kx+2與橢圓交于P、Q兩點，且OP⊥OQ，求實數k的值．

【題目】在三棱錐中，OA、OB、OC所在直線兩兩垂直，且，CA與平面AOB所成角為，D是AB中點，三棱錐的體積是．

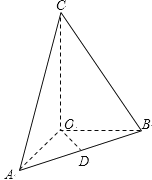
（1）求三棱錐的高；

（2）在線段CA上取一點E，當E在什么位置時，異面直線BE與OD所成的角為？

【題目】某地政府為了幫助當地農民脫貧致富,開發了一種新型水果類食品,該食品生產成本為每件8元.當天生產當天銷售時,銷售價為每件12元,當天未賣出的則只能賣給水果罐頭廠,每件只能賣5元.每天的銷售量與當天的氣溫有關,根據市場調查,若氣溫不低于,則銷售5000件;若氣溫位于,則銷售3500件;若氣溫低于,則銷售2000件.為制定今年8月份的生產計劃,統計了前三年8月份的氣溫范圍數據,得到下面的頻數分布表:

以氣溫范圍位于各區間的頻率代替氣溫范圍位于該區間的概率.

(1)求今年8月份這種食品一天銷售量(單位:件)的分布列和數學期望值;

(2)設8月份一天銷售這種食品的利潤為(單位:元),當8月份這種食品一天生產量(單位:件)為多少時,的數學期望值最大,最大值為多少

【題目】半圓的直徑的兩端點為,點在半圓及直徑上運動,若將點的縱坐標伸長到原來的2倍(橫坐標不變)得到點,記點的軌跡為曲線.

(1)求曲線的方程;

(2)若稱封閉曲線上任意兩點距離的最大值為該曲線的“直徑”,求曲線的“直徑”.

【題目】太極圖是由黑白兩個魚形紋組成的圖案，俗稱陰陽魚，太極圖展現了一種相互轉化，相對統一的和諧美，定義：能夠將圓的周長和面積同時等分成兩個部分的函數稱為圓的一個“太極函數”，則下列有關說法中：

①對于圓的所有非常數函數的太極函數中，都不能為偶函數；

②函數是圓的一個太極函數；

③直線所對應的函數一定是圓的太極函數；

④若函數是圓的太極函數，則

所有正確的是__________．

（i）老年人的人數多于中年人的人數;

（ii）中年人的人數多于青年人的人數;

（iii）青年人的人數的兩倍多于老年人的人數.

①若青年人的人數為4,則中年人的人數的最大值為___________.

②抽取的總人數的最小值為__________．

【題目】在正四棱錐中，已知異面直線與所成的角為，給出下面三個命題:

:若，則此四棱錐的側面積為；

：若分別為的中點，則平面；

:若都在球的表面上，則球的表面積是四邊形面積的倍.

在下列命題中，為真命題的是（ ）

A. B. C. D.

記甲法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為，和，記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為，和，則下面說法正確的是

A. ，，B. ，，

C. ，，D. ，，