
科目: 來源: 題型:
【題目】某小區樓頂成一種“楔體”形狀,該“楔體”兩端成對稱結構,其內部為鋼架結構(未畫出全部鋼架,如圖1所示,俯視圖如圖2所示),底面![]() 是矩形,
是矩形,![]() 米,
米,![]() 米,屋脊
米,屋脊![]() 到底面
到底面![]() 的距離即楔體的高為1.5米,鋼架所在的平面
的距離即楔體的高為1.5米,鋼架所在的平面![]() 與
與![]() 垂直且與底面的交線為
垂直且與底面的交線為![]() ,
,![]() 米,
米,![]() 為立柱且O是
為立柱且O是![]() 的中點.
的中點.
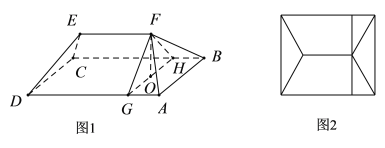
(1)求斜梁![]() 與底面
與底面![]() 所成角的大小(結果用反三角函數值表示);
所成角的大小(結果用反三角函數值表示);
(2)求此模體![]() 的體積.
的體積.
查看答案和解析>>
科目: 來源: 題型:
【題目】定義域均為D的三個函數![]() ,
,![]() ,
,![]() 滿足條件:對任意
滿足條件:對任意![]() ,點
,點![]() 與點
與點![]() 都關于點
都關于點![]() 對稱,則稱
對稱,則稱![]() 是
是![]() 關于
關于![]() 的“對稱函數”.已知函數
的“對稱函數”.已知函數![]() ,
,![]() ,
,![]() 是
是![]() 關于
關于![]() 的“對稱函數“,記
的“對稱函數“,記![]() 的定義域為D,若對任意
的定義域為D,若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,則實數a的取值范圍是( )
成立,則實數a的取值范圍是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】已知平面![]() ,B,
,B,![]() ,
,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,則下列敘述錯誤的是( )
,則下列敘述錯誤的是( )
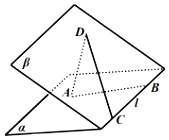
A.直線![]() 與
與![]() 是異面直線
是異面直線
B.直線![]() 在
在![]() 上的射影可能與
上的射影可能與![]() 平行
平行
C.過![]() 有且只有一個平面與
有且只有一個平面與![]() 平行
平行
D.過![]() 有且只有一個平面與
有且只有一個平面與![]() 垂直
垂直
查看答案和解析>>
科目: 來源: 題型:
【題目】在傳染病學中,通常把從致病刺激物侵入機體或者對機體發生作用起,到機體出現反應或開始呈現該疾病對應的相關癥狀時止的這一階段稱為潛伏期.
(1)一研究團隊統計了某地區1000名患者的相關信息,得到如下表格,

該傳染病的潛伏期受諸多因素影響,為研究潛伏期與患者年齡的關系,以潛伏期是否超過6天為標準進行分層抽樣,從上述1000名患者中抽取200人,得到如下列聯表,請將列聯表補充完整,并根據列聯表判斷是否有95%的把握認為潛伏期與患者年齡有關
潛伏期≤6天 | 潛伏期>6天 | 總計 | |
50歲以上(含50歲) | 100 | ||
50歲以下 | 55 | ||
總計 | 200 |
(2)以這1000名患者的潛伏期超過6天的頻率,代替該地區1名患者潛伏期超過6天發生的概率,每名患者的潛伏期是否超過6天相互獨立.為了深入研究,該研究團隊隨機調查了20名患者,其中潛伏期超過6天的人數最有可能(即概率最大)是多少?
附:下面的臨界值表僅供參考.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
(參考公式: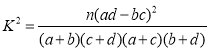 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目: 來源: 題型:
【題目】
如圖,在四面體![]() 中,
中,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 、
、![]() 分別是
分別是![]() 和
和![]() 上的動點,且
上的動點,且![]() 與
與![]() 相交于點
相交于點![]() .下列判斷中:
.下列判斷中:
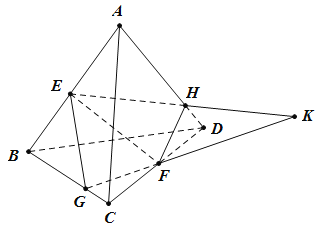
①直線![]() 經過點
經過點![]() ;
;
②![]() ;
;
③![]() 、
、![]() 、
、![]() 、
、![]() 四點共面,且該平面把四面體
四點共面,且該平面把四面體![]() 的體積分為相等的兩部分.
的體積分為相等的兩部分.
所有正確的序號為
__________.
查看答案和解析>>
科目: 來源: 題型:
【題目】勒洛三角形是具有類似圓的“定寬性”的曲線,它是由德國機械工程專家、機構運動學家勒洛首先發現,其作法是:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形.如圖中的兩個勒洛三角形,它們所對應的等邊三角形的邊長比為![]() ,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率是( )
,若從大的勒洛三角形中隨機取一點,則此點取自小勒洛三角形內的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.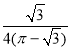
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com