
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,且
上的點,且![]() 平面
平面![]() .
.
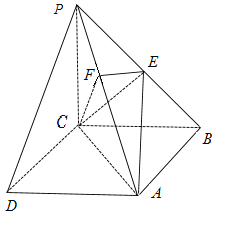
(Ⅰ)求證:![]() 為
為![]() 的中點;
的中點;
(Ⅱ)當![]() 與平面
與平面![]() 所成的角最大時,求二面角
所成的角最大時,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)證明見詳解;(Ⅱ)![]()
【解析】
(Ⅰ)利用線面平行的性質定理可得![]() ,再根據三角形的中位線性質即可證出.
,再根據三角形的中位線性質即可證出.
(Ⅱ)首先作出線面角,利用三角形的面積相等可得![]() ,以
,以![]() 為坐標原點,
為坐標原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系,求出平面
軸,建立空間直角坐標系,求出平面![]() 的一個法向量與平面
的一個法向量與平面![]() 的一個法向量,利用空間向量的數量積即可求解.
的一個法向量,利用空間向量的數量積即可求解.
(Ⅰ)連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,
,
平面![]() 平面
平面![]()
![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
則![]() ,
,
![]() 底面
底面![]() 是正方形,點
是正方形,點![]() 為
為![]() 的中點,
的中點,
![]()
![]() 為
為![]() 的中點.
的中點.
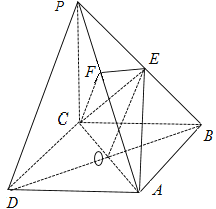
(Ⅱ)由底面![]() 是正方形,且
是正方形,且![]() ,則
,則![]() ,
,
又![]() 底面
底面![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
在平面![]() 內,過
內,過![]() 作
作![]() ,連接
,連接![]() ,
,
則![]() 與平面
與平面![]() 所成的角
所成的角![]() 最大.
最大.
設![]() ,則
,則![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() ,
,
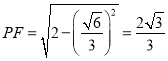 ,即
,即![]() ,
,
以![]() 為坐標原點,
為坐標原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,
建立空間直角坐標系,如圖:
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則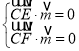 ,即
,即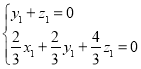 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
所以![]() ,、
,、
設平面![]() 的一個法向量
的一個法向量![]() ,
,
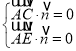 ,即
,即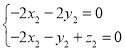 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
所以![]()
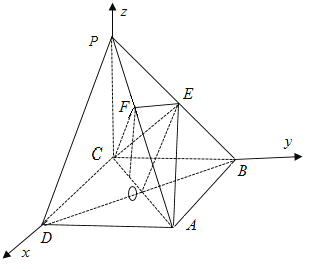
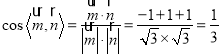 ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
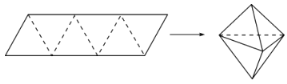
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽粒,古稱角黍,是端午節大家都會品嘗的食品.如圖,平行四邊形形狀的紙片是由六個邊長為2的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為_________;若該六面體內有一球,當該球體積最大時,球的表面積是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人們生活水平的不斷提高,肥胖人數不斷增多.世界衛生組織(WHO)常用身體質量指數(BMI)來衡量人體胖瘦成度以及是否健康,其計算公式是![]() .成人的BMI數值標準為:BMI
.成人的BMI數值標準為:BMI![]() 偏瘦;
偏瘦;![]() BMI
BMI![]() 為正常;
為正常;![]() BMI
BMI![]() 為偏胖;BMI
為偏胖;BMI![]() 為肥胖.某研究機構為了解某快遞公司員工的身體質量指數,研究人員從公司員工體檢數據中,抽取了8名員工(編號1-8)的身高
為肥胖.某研究機構為了解某快遞公司員工的身體質量指數,研究人員從公司員工體檢數據中,抽取了8名員工(編號1-8)的身高![]() (cm)和體重
(cm)和體重![]() (kg)數據,并計算得到他們的BMI(精確到0.1)如下表:
(kg)數據,并計算得到他們的BMI(精確到0.1)如下表:
編 號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
體重(kg) | 54 | 60 | 77 | 72 | 68 | ● | 72 | 55 |
BMI(近似值) | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
(1)現從這8名員工中選取3人進行復檢,記抽取到BMI值為“正常”員工的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
(2)研究機構分析發現公司員工的身高![]() (cm)和體重
(cm)和體重![]() (kg)之間有較強的線性相關關系,在編號為6的體檢數據丟失之前調查員甲已進行相關的數據分析,并計算得出該組數據的線性回歸方程為
(kg)之間有較強的線性相關關系,在編號為6的體檢數據丟失之前調查員甲已進行相關的數據分析,并計算得出該組數據的線性回歸方程為![]() ,且根據回歸方程預估一名身高為180cm的員工體重為71kg,計算得到的其它數據如下:
,且根據回歸方程預估一名身高為180cm的員工體重為71kg,計算得到的其它數據如下:![]() ,
,![]() .
.
①求![]() 的值及表格中8名員工體重的平均值
的值及表格中8名員工體重的平均值![]() .
.
②在數據處理時,調查員乙發現編號為8的員工體重數據有誤,應為63kg,身高數據無誤,請你根據調查員乙更正的數據重新計算線性回歸方程,并據此預估一名身高為180cm的員工的體重.
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: 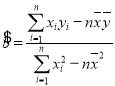 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義域均為D的三個函數![]() ,
,![]() ,
,![]() 滿足條件:對任意
滿足條件:對任意![]() ,點
,點![]() 與點
與點![]() 都關于點
都關于點![]() 對稱,則稱
對稱,則稱![]() 是
是![]() 關于
關于![]() 的“對稱函數”.已知函數
的“對稱函數”.已知函數![]() ,
,![]() ,
,![]() 是
是![]() 關于
關于![]() 的“對稱函數“,記
的“對稱函數“,記![]() 的定義域為D,若對任意
的定義域為D,若對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,則實數a的取值范圍是( )
成立,則實數a的取值范圍是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
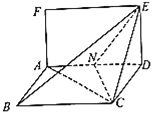
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
, ![]() ,
, ![]() ,點
,點![]() 為線段
為線段![]() 的中點.
的中點.
(Ⅰ)試問在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() ?若存在,請證明
?若存在,請證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“二進制”來源于我國古代的《易經》,該書中有兩類最基本的符號:“─”和“﹣﹣”,其中“─”在二進制中記作“1”,“﹣﹣”在二進制中記作“0”.如符號“”對應的二進制數011(2)化為十進制的計算如下:011(2)=0×22+1×21+1×20=3(10).若從兩類符號中任取2個符號進行排列,則得到的二進制數所對應的十進制數大于2的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為抑制房價過快上漲和過度炒作,各地政府響應中央號召,因地制宜出臺了系列房價調控政策.某市擬定出臺“房產限購的年齡政策”.為了解人們對“房產限購年齡政策”的態度,在2060歲的人群中隨機調查100人,調查數據的頻率分布直方圖和支持“房產限購”的人數與年齡的統計結果如圖所示:
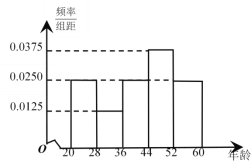
年齡 |
|
|
|
|
|
支持的人數 | 15 | 5 | 15 | 28 | 17 |
(1)由以上統計數據填![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以44歲為分界點的不同人群對“房產限購年齡政策”的支持度有差異?
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以44歲為分界點的不同人群對“房產限購年齡政策”的支持度有差異?
44歲以下 | 44歲及44歲以上 | 總計 | |
支持 | |||
不支持 | |||
總計 |
(2)若以44歲為分界點,從不支持“房產限購”的人中按分層抽樣的方法抽取8人參加政策聽證會,現從這8人中隨機抽2人.記抽到44歲以上的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式: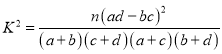 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com