日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

設函數y＝f(x)的定義域為(0，＋∞)，且對任意的正實數x，y，均有f(xy)＝f(x)＋f(y)恒成立．已知f(2)＝1，且當x＞1時，f(x)＞0．

(1)求f()的值，試判斷y＝f(x)在(0，＋∞)上的單調性，并加以證明；

(2)一個各項均為正數的數列{a_n}，它的前n項和是S_n，若a₁＝3，且f(S_n)＝f(a_n)＋f(a_n＋1)－1(n≥2，n∈N^*)，求數列{a_n}的通項公式；

(3)在(2)的條件下，是否存在實數M，使2ⁿ·a₁·a₂……a_n≥M··(2a₁－1)·(2a₂－1)……(2a_n－1)

對于一切正整數n均成立？若存在，求出M的范圍；若不存在，請說明理由．

函數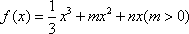在x＝1處取得極值，(x)的最小值為－4．

(1)求m，n的值及f(x)的單調區間；

(2)試分別求方程f(x)－c＝0在區間[－4，1]上有一根、有兩根時c的范圍．

設函數y＝f(x)的定義域為(0，＋∞)，且對任意的正實數x，y，均有f(xy)＝f(x)＋f(y)恒成立．已知f(2)＝1，且當x＞1時，f(x)＞0．

(1)求的值，試判斷y＝f(x)在(0，＋∞)上的單調性，并加以證明；

(2)一個各項均為正數的數列{a_n}，它的前n項和是S_n，若a₁＝3，且對任意的正整數n，均滿足，求數列{a_n}的通項公式．

選修4－5：不等式選講

已知函數f(x)＝|x－2|，g(x)＝－|x＋3|＋m

(1)解關于x的不等式f(x)＋a－1＞0(a∈R)；

(2)若函數f(x)的圖象恒在函數g(x)圖象的上方，求m的取值范圍．

已知函數，

(1)若a＝1，求函數f(x)在點(e，f(e))處的切線方程；

(2)設函數h(x)＝f(x)－g(x)，求函數h(x)的單調區間；

(3)若在[1，e](e＝2.718…)上存在一點x₀，使得f(x₀)＜g(x₀)成立，求a的取值范圍．

某種汽車的購車費用是10萬元，每年使用的保險費、養路費、汽油費約為0.9萬元，年維修費用第一年是0.2萬元，第二年是0.4萬元，第三年是0.6萬元，…，以后逐年遞增0.2萬元．汽車的購車費用、每年使用的保險費、養路費、汽油費、維修費用的和平均攤到每一年的費用叫做年平均費用．設這種汽車使用x(x∈N^*)年的維修費用為g(x)，年平均費用為f(x)．

(1)求出函數g(x)，f(x)的解析式；

(2)這種汽車使用多少年時，它的年平均費用最小？最小值是多少？

已知函數f(x)＝log₂x，設是首項和公差都等于1的等差數列．數列{b_n}滿足．

(1)求數列{a_n}的通項公式，并證明數列{b_n}不是等比數列；

(2)令，求證：S_n＜3．

選修4－4：坐標系與參數方程

已知曲線C₁：，曲線C₂：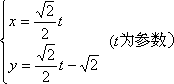

(1)曲線C₁，C₂是否有公共點，為什么？

(2)若把C₁，C₂上各點的橫坐標都壓縮為原來的一半，分別得到曲線，．問與公共點的個數和C₁與C₂公共點的個數是否相同？說明你的理由．

設x₁、x₂(x₁≠x₂)是函數f(x)＝ax³＋bx²－a²x(a＞0)的兩個極值點．

(1)若x₁＝－1，x₂＝2，求函數f(x)的解析式；

(2)若，求b的最大值．

(3)若x₁＜x＜x₂，且x₂＝a，，求證：．

如圖，已知橢圓的上頂點為A，右焦點為F，直線AF與圓M：x²＋y²－6x－2y＋7＝0相切．

(Ⅰ)求橢圓C的方程；

(Ⅱ)若不過點A的動直線l與橢圓C相交于P、Q兩點，且求證：直線l過定點，并求出該定點N的坐標