
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 將條件“?x∈[0,$\frac{π}{3}$],tanx≤m”轉化為“x∈[0,$\frac{π}{3}$]時,m≥(tanx)max”,再利用y=tanx在[0,$\frac{π}{3}$]的單調性求出tanx的最大值即可.
解答 解:∵“?x∈[0,$\frac{π}{3}$],tanx≤m”是真命題,
∴x∈[0,$\frac{π}{3}$]時,m≥(tanx)max,
∵y=tanx在[0,$\frac{π}{3}$]的單調遞增,
∴x=$\frac{π}{3}$時,tanx取得最大值為$\sqrt{3}$,
∴$m≥\sqrt{3}$,即m的最小值為$\sqrt{3}$.
故選:D.
點評 本題主要考查了轉化思想,將恒成立問題轉化為最值問題,再通過正切函數的單調性求出函數的最值即可,屬于中檔題.


 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (3,-4) | B. | (-4,3) | C. | (4,-3) | D. | (-3,-4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
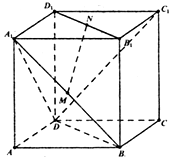 如圖,在正方體ABCD-A1B1C1D1中,點M、N分別是面對角線A1B與B1D1的中點,設$\overrightarrow{DA}$=$\overrightarrow a$,$\overrightarrow{DC}$=$\overrightarrow b$,$\overrightarrow{D{D_1}}$=$\overrightarrow c$.
如圖,在正方體ABCD-A1B1C1D1中,點M、N分別是面對角線A1B與B1D1的中點,設$\overrightarrow{DA}$=$\overrightarrow a$,$\overrightarrow{DC}$=$\overrightarrow b$,$\overrightarrow{D{D_1}}$=$\overrightarrow c$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| 分組(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 頻數(個) | 10 | 50 | m | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com