
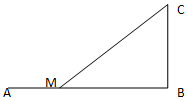
 如圖,設鐵路AB長為50,BC⊥AB,且BC=10,為將貨物從A運往C,現在AB上距點B為x的點M處修一公路至C,已知單位距離的鐵路運費為2,公路運費為4.
如圖,設鐵路AB長為50,BC⊥AB,且BC=10,為將貨物從A運往C,現在AB上距點B為x的點M處修一公路至C,已知單位距離的鐵路運費為2,公路運費為4.分析 (1)由已知中鐵路AB長為50,BC⊥AB,且BC=10,為將貨物從A運往C,現在AB上距點B為x的點M處修一公路至C,已知單位距離的鐵路運費為2,公路運費為4,我們可計算出公路上的運費和鐵路上的運費,進而得到由A到C的總運費;
(2)由(1)中所得的總運費y表示為x的函數,利用導數法,我們可以分析出函數的單調性,及函數的最小值點,得到答案.
解答 解:(1)依題中,鐵路AB長為50,BC⊥AB,且BC=10,
將貨物從A運往C,現在AB上距點B為x的點M處修一公路至C,
且單位距離的鐵路運費為2,公路運費為4
∴鐵路AM上的運費為2(50-x),公路MC上的運費為4 $\sqrt{100{+x}^{2}}$,
則由A到C的總運費為y=2(50-x)+4 $\sqrt{100{+x}^{2}}$(0≤x≤50)…(6分)
(2)y′=-2+$\frac{4x}{\sqrt{100{+x}^{2}}}$(0≤x≤50),
令y′=0,
解得x=$\frac{10}{\sqrt{3}}$,或x=-$\frac{10}{\sqrt{3}}$(舍)…(9分)
當0≤x≤$\frac{10}{\sqrt{3}}$時,y′≤0;當$\frac{10}{\sqrt{3}}$≤x≤50時,y′≥0
故當x=$\frac{10}{\sqrt{3}}$時,y取得最小值.…(12分)
即當在距離點B為$\frac{10}{\sqrt{3}}$時的點M處修筑公路至C時總運費最省.…(13)
點評 本題考查的知識點是導數在最大值最小值問題中的應用,函數最值的應用,其中根據已知條件求出函數的解析式,并確定函數的單調性是解答本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,矩形O′A′B′C′是水平放置的一個平面圖形的直觀圖,其中O′A′=6,O′C′=2,則原圖形OABC的面積為24$\sqrt{2}$.
如圖,矩形O′A′B′C′是水平放置的一個平面圖形的直觀圖,其中O′A′=6,O′C′=2,則原圖形OABC的面積為24$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {7} | B. | {5,7} | C. | {3,5,7} | D. | {x|6<x≤7} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com