Question

13．如圖，AB是圓O的直徑，點C是圓O上異于A、B的點，直線度PC⊥平面ABC，E、F分別是PA、PC的中點．
（Ⅰ）設平面BEF與平面ABC的交線為l，求直線l與平面PBC所成角的余弦值；
（Ⅱ）設（Ⅰ）中的直線l與圓O的另一個交點為點D，且滿足$\overrightarrow{DQ}=λ\overrightarrow{CP}$，$∠ABC=∠CBP=\frac{π}{3}$，當二面角Q-BC-P的余弦值為$\frac{{\sqrt{3}}}{3}$時，求λ的值．

Answer 1

分析 （I）直線l∥平面PAC．連接EF，利用三角形的中位線定理可得，EF∥AC；利用線面平行的判定定理即可得到EF∥平面ABC．由線面平行的性質定理可得EF∥l．再利用l∥EF∥AC，得直線l與平面PBC所成角α為直角，
（Ⅱ）以點C為原點，向量$\overrightarrow{CA}$，$\overrightarrow{CB}$，$\overrightarrow{CP}$所在直線分別為x，y，z軸，建立如圖所示的空間直角坐標系，
則A（$\sqrt{3}$，0，0），B（0，1，0），D（$\sqrt{3}$，1，0），P（0，0，$\sqrt{3}$），$Q（\sqrt{3}，1，\sqrt{3}λ）$，利用兩個平面的法向量的夾角即可得出二面角．求出λ

解答 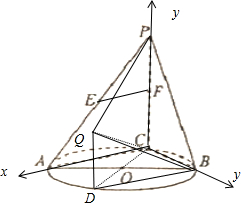解：（Ⅰ）過B作AC的平行線BD，交線l即為直線BD，且l∥AC
∵PC⊥平面ABC，∴PC⊥BC，
又∵AC⊥BC，∴BC⊥平面PBC，
∵E，F分別是PA，PC的中點，所以EF∥AC，
又∵EF?平面ABC，AC?平面ABC，
∴EF∥面ABC，
又∵EF?平面BEF，平面BEF∩平面ABC=l，
∴直線EF∥直線l，∴l∥EF∥AC，且AC⊥面PBC，
∴直線l與平面PBC所成角α為直角，cosα=0．
（Ⅱ）設CB=1，則$CA=\sqrt{3}=CP$，如圖作DQ∥CP，且DQ=λPC．
連接PQ，EF，BE，BF，BD，由（Ⅰ）可知交線l即為直線BD．
以點C為原點，向量$\overrightarrow{CA}$，$\overrightarrow{CB}$，$\overrightarrow{CP}$所在直線分別為x，y，z軸，建立如圖所示的空間直角坐標系，
則A（$\sqrt{3}$，0，0），B（0，1，0），D（$\sqrt{3}$，1，0），P（0，0，$\sqrt{3}$），$Q（\sqrt{3}，1，\sqrt{3}λ）$，
易得面PBC的一個法向量為$\overrightarrow{n_1}=（1，0，0）$，
設面QBC的一個法向量為$\overrightarrow{{n}_{2}}=（x，y，z）$，
$\overrightarrow{CB}=（0，1，0）$，$\overrightarrow{CQ}=（\sqrt{3}，1，\sqrt{3}λ）$，由$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{CB}=y=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{CQ}=\sqrt{3}x+y+\sqrt{3}λz=0}\end{array}\right.$，
可求出面QBC的一個法向量$\overrightarrow{n_2}=（-λ，0，1）$，
|cos$＜\overrightarrow{{n}_{1}}，\overrightarrow{{n}_{2}}＞$|=$\frac{λ}{1×\sqrt{{λ}^{2}+1}}=\frac{\sqrt{3}}{3}$，
可得$λ=\frac{{\sqrt{2}}}{2}$．

點評 本題綜合考查了線面平行的判定定理和性質定理、線面垂直的判定與性質定理、二面角、通過建立空間直角坐標系利用法向量的夾角求二面角等基礎知識與方法，需要較強的空間想象能力、推理能力和計算能力．屬于中檔題．