
【題目】已知函數f(x)為二次函數,且f(x﹣1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)當x∈[t,t+2],t∈R時,求函數f(x)的最小值(用t表示).
【答案】
(1)解:設f(x)=ax2+bx+c,
![]()
∴ 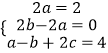
解得∴ ![]()
∴f(x)=x2+x+2
(2)解:∵f(x)=x2+x+2的對稱軸為 ![]() ;
;
當 ![]() 即
即 ![]() 時
時 ![]() ;
;
當 ![]() 時,f(x)=x2+x+2在x∈[t,t+2]上單調遞增,
時,f(x)=x2+x+2在x∈[t,t+2]上單調遞增, ![]() ;
;
當 ![]() 時,f(x)=x2+x+2在x∈[t,t+2]上單調遞減,
時,f(x)=x2+x+2在x∈[t,t+2]上單調遞減, ![]() ;
;
綜上:f(x)min= 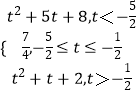
【解析】(1)首先設出函數的解析式,利用待定系數法即可;(2)判斷函數f(x)的對稱軸與區間[t,t+2]的位置關系,再根據圖形特征求出最小值;
【考點精析】根據題目的已知條件,利用二次函數的性質的相關知識可以得到問題的答案,需要掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為(﹣1,1),對任意x,y∈(﹣1,1),有f(x)+f(y)=f( ![]() ).且當x<0時,f(x)>0.
).且當x<0時,f(x)>0.
(1)驗證函數f(x)=lg ![]() 是否滿足這些條件;
是否滿足這些條件;
(2)若f( ![]() )=1,f(
)=1,f( ![]() )=2,且|a|<1,|b|<1,求f(a),f(b)的值.
)=2,且|a|<1,|b|<1,求f(a),f(b)的值.
(3)若f(﹣ ![]() )=1,試解關于x的方程f(x)=﹣
)=1,試解關于x的方程f(x)=﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l過點P(0,﹣4),且傾斜角為 ![]() ,圓C的極坐標方程為ρ=4cosθ.
,圓C的極坐標方程為ρ=4cosθ.
(1)求直線l的參數方程和圓C的直角坐標方程;
(2)若直線l和圓C相交于A、B兩點,求|PA||PB|及弦長|AB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1.
,AB=2,PA=1. 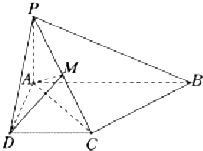
(1)求證:BC⊥平面PAC;
(2)若M是PC的中點,求二面角M﹣AD﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,曲線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 、
、![]() 的極坐標方程;
的極坐標方程;
(2)求曲線![]() 與
與![]() 交點的極坐標,其中
交點的極坐標,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名運動員參加“選拔測試賽”,在相同條件下,兩人6次測試的成績(單位:分)記錄如下:
甲 86 77 92 72 78 84
乙 78 82 88 82 95 90
(1)用莖葉圖表示這兩組數據,現要從中選派一名運動員參加比賽,你認為選派誰參賽更好?說明理由(不用計算);
(2)若將頻率視為概率,對運動員甲在今后三次測試成績進行預測,記這三次成績高于85分的次數為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com