
分析 (1)設出二次函數的一般形式后,代入f(x+1)=f(x)+x+1,化簡后根據多項式相等,各系數相等即可求出a,b及c的值,即可確定出f(x)的解析式;
(2)對稱軸x=-$\frac{1}{2}$,討論區間與對稱軸的位置關系,從而求最小值.
(3))由g(t)+m≥0對t∈R恒成立,可得-m≤g(t)min,由(2)可知g(t)min=-$\frac{1}{8}$,問題得以解決.
解答 解:(1)令f(x)=ax2+bx+c,(a≠0)
代入f(x+1)=f(x)+x+1,
得:a(x+1)2+b(x+1)+c=ax2+bx+c+x+1,
∴(2a+b)x+a+b=(b+1)x+1,
∴$\left\{\begin{array}{l}{2a+b=b+1}\\{a+b=1}\end{array}\right.$,
解得a=$\frac{1}{2}$,b=$\frac{1}{2}$
又∵f(0)=c=0
∴f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x,
(2)由(1)可得f(x)的對稱軸為x=-$\frac{1}{2}$,
∴函數f(x)在(-∞,-$\frac{1}{2}$)單調遞減,在($\frac{1}{2}$,+∞)單調遞增,
①當t+1≤-$\frac{1}{2}$,即t≤-$\frac{3}{2}$時,f(x)在[t,t+1]單調遞減,
g(t)=f(x)min=f(t+1)=$\frac{1}{2}$t2+$\frac{3}{2}$t+1,
②-$\frac{1}{2}$<t+1且t<-$\frac{1}{2}$,即-$\frac{3}{2}$<t<-$\frac{1}{2}$時,f(x)在[t,-$\frac{1}{2}$)遞減,在(-$\frac{1}{2}$,t+1]遞增,
∴g(t)=f(x)min=f(-$\frac{1}{2}$)=-$\frac{1}{8}$,
③t≥-$\frac{1}{2}$時,函數f(x)在[t,t+1]單調遞增,
∴g(t)=f(x)min=f(t)=$\frac{1}{2}$t2+$\frac{1}{2}$t,
∴g(t)=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}+\frac{3}{2}t+1,t≤-\frac{3}{2}}\\{-\frac{1}{8},-\frac{3}{2}<t<-\frac{1}{2}}\\{\frac{1}{2}{t}^{2}+\frac{1}{2}t.t≥-\frac{1}{2}}\end{array}\right.$,
(3)∵g(t)+m≥0對t∈R恒成立,
∴-m≤g(t)min,
由(2)可知g(t)min=-$\frac{1}{8}$,
∴-m≤-$\frac{1}{8}$,
∴m≥$\frac{1}{8}$.
點評 本題考查的知識點是函數解析式的求法,及二次函數在閉區間上的最值,熟練掌握待定系數法求函數解析式的步驟及二次函數的圖象和性質是解答的關鍵.


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
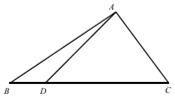 如圖,在△ABC中,點D在BC邊上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.
如圖,在△ABC中,點D在BC邊上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
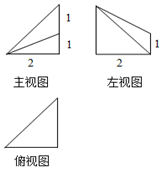
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,在正方體ABCD-A1B1C1D1中,O為底面ABCD的中心,P是DD1的中點,設Q是CC1上的點.
如圖所示,在正方體ABCD-A1B1C1D1中,O為底面ABCD的中心,P是DD1的中點,設Q是CC1上的點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com