
分析 (1)若函數的定義域為R,則(m2-1)x2-(1-m)x+1>0對x∈R恒成立,進而可得實數m的取值范圍;
(2)若函數的值域為R,則g(x)=(m2-1)x2-(1-m)x+1的值域包含(0,+∞),進而可得實數m的取值范圍.
解答 解:(1)由題知(m2-1)x2-(1-m)x+1>0對x∈R恒成立.
(I)當m2-1=0時,若m=1,有1>0恒成立,符合題意:
若m=-1,有$x<\frac{1}{2}$,不合題意.
(II)當m2-1≠0即m≠±1時,
有$\left\{\begin{array}{l}{m^2}-1>0⇒m>1或m<-1\\△={(1-m)^2}-4({m^2}-1)<0⇒m>1或m<-\frac{5}{3}\end{array}\right.$解得:m>1或$m<-\frac{5}{3}$;
∴由(I)(II)可知$m∈(-∞,-\frac{5}{3})∪[1,+∞)$.
(2)由題意,g(x)=(m2-1)x2-(1-m)x+1的值域包含(0,+∞),
(I)當m2-1=0時,若m=1,有g(x)=1,不合題意;
若m=-1,則g(x)=-2x+1,符合題意.
(II)當m2-1≠0即m≠±1時
有$\left\{\begin{array}{l}{m^2}-1>0\\△≥0\end{array}\right.$解得:$-\frac{5}{3}≤m<-1$
∴由(I)(II)可知$m∈[-\frac{5}{3},-1]$.
點評 本題考查的知識點是函數恒成立問題,二次函數的圖象和性質,對數函數的圖象和性質,難度中檔.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | $\frac{2015}{672}$ | D. | $\frac{2015}{336}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
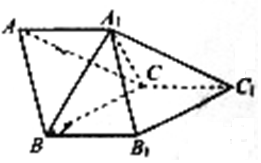 如圖所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,則下列結論正確的是( )
如圖所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,則下列結論正確的是( )| A. | :當AA1=$\frac{\sqrt{42}}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{3\sqrt{7}}{7}$ | |
| B. | :當AA1=$\frac{6}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{3\sqrt{7}}{7}$ | |
| C. | :當AA1=$\frac{\sqrt{42}}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{6}{7}$$\sqrt{7}$ | |
| D. | :當AA1=$\frac{6}{7}$時,三棱柱ABC-A1B1C1體積取得最大值,最大值為$\frac{6}{7}$$\sqrt{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
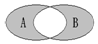 如圖所示,A、B是兩個非空集合,定義A*B表示陰影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},則A*B=( )
如圖所示,A、B是兩個非空集合,定義A*B表示陰影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},則A*B=( )| A. | [0,+∞) | B. | [0,1]∪(3,+∞) | C. | [0,1)∪[3,+∞) | D. | (1,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com