
| A. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | B. | f(x)=2x+1,g(x)=2x-1 | C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=1,g(x)=x0 |
分析 根據兩個函數的定義域相同,對應關系也相同,判斷它們是同一函數即可
解答 解:對于A:f(x)=x的定義域為R;而g(x)=$\frac{{x}^{2}}{x}$的定義域為{x|x≠0},定義域不同,∴不是同一函數;
對于B:f(x)=2x+1的定義域為R,g(x)=2x-1的定義域為R,但對應關系不同,∴不是同一函數;
對于C:f(x)=x的定義域為R,g(x)=$\root{3}{{x}^{3}}$=x的定義域為R,定義域相同,對應關系也相同,∴是同一函數;
對于D:f(x)=1的定義域為R,g(x)=x0的定義域為{x|x≠0},定義域不同,∴不是同一函數;
故選:C.
點評 本題考查了判斷兩個函數是否為同一函數的問題,是基礎題目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x≥-1或x≤-2} | B. | {x|-2≤x≤-1} | C. | {x|1≤x≤2} | D. | {x|x≥-1或x<-2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\sqrt{3}$或$\frac{\sqrt{3}}{9}$ | C. | $\frac{\sqrt{3}}{9}$ | D. | $\sqrt{3}$或$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
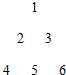 把正整數按上小下大、左小右大的原則排成如圖三角形數表(每行比上一行多一個數):設ai,j(i、j∈N*)是位于這個三角形數表中從上往下數第i行、從左往右數第j個數,如a4,2=8.若ai,j=2015,則i、j的值分別為63,62.
把正整數按上小下大、左小右大的原則排成如圖三角形數表(每行比上一行多一個數):設ai,j(i、j∈N*)是位于這個三角形數表中從上往下數第i行、從左往右數第j個數,如a4,2=8.若ai,j=2015,則i、j的值分別為63,62.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com