
已知函數 ,其中
,其中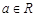 .
.
(1)若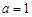 ,求函數
,求函數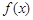 的極值點;
的極值點;
(2)若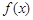 在區間
在區間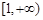 內單調遞增,求實數
內單調遞增,求實數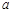 的取值范圍.
的取值范圍.
(1)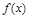 有極小值點
有極小值點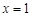 ,無極大值點;(2)[1,+∞)。
,無極大值點;(2)[1,+∞)。
解析試題分析:(1)先求出函數的定義域,求出函數的導數,求出導數為0的點,確定導數為0和導數不存在點的點的左右兩側導函數的符號,確定函數的單調性,若單調性相同不是極值點,若左增右減是極大值點,若左減右增是極小值點;(2)先求出導數,利用導數與函數單調性關系,將函數在[1,+∞)上是增函數問題轉化為導函數大于等于0在[1,+∞)上恒成立問題,通過參變分離,轉化為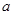 ≥
≥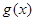 在[1,+∞)恒成立問題,求出
在[1,+∞)恒成立問題,求出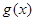 在[1,+∞)的最大值
在[1,+∞)的最大值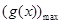 ,則
,則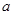 ≥
≥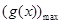 .
.
試題解析:(1)當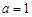 時,
時,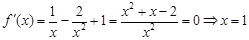 或
或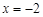 ……3分
……3分
所以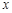
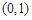
1 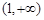
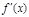
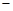
0 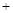
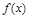
單調減 極小值 單調增 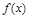 有極小值點
有極小值點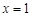 ,無極大值點……6分
,無極大值點……6分
(2)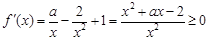 ,所以
,所以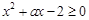
 對
對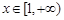 恒成立……9分
恒成立……9分
又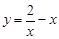 在
在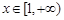 上單調遞減,所以
上單調遞減,所以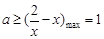 .……12分
.……12分
考點:1.利用導數求函數極值;2.函數單調性與導數關系;3.轉化與化歸思想.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com