
分析 (1)先求導,再令f'(x)=0得到x=-1或aex-2a+2=0(*),根據aex-2a+2=0(*)無解即可求出a的范圍.
(2)求出-2<x1<-1,-1<x2<0,根據$f({x_1})=a{x_1}{e^{x_1}}-({a-1}){({{x_1}+1})^2}=0,f({x_2})=a{x_2}{e^{x_2}}-({a-1}){({{x_2}+1})^2}=0$,得到-3<x1+x2<-1,問題轉化為證明f(x1)>f(-2-x2)即可.
解答 (1)解:f'(x)=aex+axex-2(a-1)(x+1)=(x+1)(aex-2a+2),
由f'(x)=0得到x=-1或aex-2a+2=0(*)
由于f(x)僅有一個極值點,
關于x的方程(*)必無解,
①當a=0時,(*)無解,符合題意,
②當a≠0時,由(*)得${e^x}=\frac{2a-2}{a}$,故由$\frac{2a-2}{a}≤0$得0<a≤1,
由于這兩種情況都有,當x<-1時,f'(x)<0,于是f(x)為減函數,
當x>-1時,f'(x)>0,于是f(x)為增函數,
∴僅x=-1為f(x)的極值點,綜上可得a的取值范圍是[0,1];
(2)證明:由(1)當$0<a<\frac{1}{2}$時,x=-1為f(x)的極小值點,
又∵$f({-2})=-\frac{2a}{e^2}-({a-1})=({-\frac{2}{e^2}-1})a+1>0$對于$0<a<\frac{1}{2}$恒成立,
$f({-1})=-\frac{a}{e}<0$對于$0<a<\frac{1}{2}$恒成立,
f(0)=-(a-1)>0對于$0<a<\frac{1}{2}$恒成立,
∴當-2<x<-1時,f(x)有一個零點x1,
當-1<x<0時,f(x)有另一個零點x2,
即-2<x1<-1,-1<x2<0,
且$f({x_1})=a{x_1}{e^{x_1}}-({a-1}){({{x_1}+1})^2}=0,f({x_2})=a{x_2}{e^{x_2}}-({a-1}){({{x_2}+1})^2}=0$,(#)
所以-3<x1+x2<-1,
下面再證明x1+x2<-2,即證x1<-2-x2,
由-1<x2<0得-2<-2-x2<-1,
由于x<-1,f(x)為減函數,
于是只需證明f(x1)>f(-2-x2),
也就是證明f(-2-x2)<0,$f({-2-{x_2}})=a({-2-{x_2}}){e^{-2-{x_2}}}-({a-1}){({-{x_2}-1})^2}=a({-2-{x_2}}){e^{-2-{x_2}}}-({a-1}){({{x_2}+1})^2}$,
借助(#)代換可得$f({-2-{x_2}})=a({-2-{x_2}}){e^{-2-{x_2}}}-a{x_2}{e^{x_2}}=a[{({-2-{x_2}}){e^{-2-{x_2}}}-{x_2}{e^{x_2}}}]$,
令g(x)=(-2-x)e-2-x-xex(-1<x<0),
則g'(x)=(x+1)(e-2-x-ex),
∵h(x)=e-2-x-ex為(-1,0)的減函數,且h(-1)=0,
∴g'(x)=(x+1)(e-2-x-ex)<0在(-1,0)恒成立,
于是g(x)為(-1,0)的減函數,即g(x)<g(-1)=0,
∴f(-2-x2)<0,這就證明了x1+x2<-2,
綜上所述,-3<x1+x2<-2.
點評 本題考查了導數和函數的單調性和關系和一級函數的極值的問題,考查了分類討論的思想以及不等式的證明,是一道綜合題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
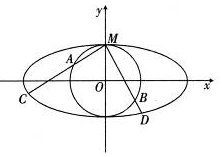 如圖,圓O(O為坐標原點)與離心率為$\frac{{\sqrt{3}}}{2}$的橢圓T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于點M(0,1).
如圖,圓O(O為坐標原點)與離心率為$\frac{{\sqrt{3}}}{2}$的橢圓T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于點M(0,1). 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com