
| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
分析 利用線性規劃的內容作出不等式組對應的平面區域,然后由z=4x+y得y=-4x+z,根據平移直線確定目標函數的最大值.
解答 解:作出不等式組對應的平面區域如圖: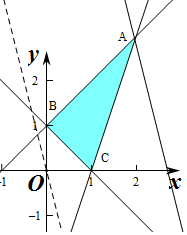
由z=4x+y得y=-4x+z,平移直線y=-4x+z,
由圖象可知當直線經過點A時,直線的截距最大,此時Z最大,
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x-y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
代入z=4x+y得最大值為z=4×2+3=11.
故選:B.
點評 本題主要考查二元一次不等式組表示平面區域的知識,以及線性規劃的基本應用,利用數形結合是解決此類問題的關鍵.


科目:高中數學 來源: 題型:解答題
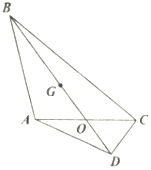 如圖,在平面四邊形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如圖,在平面四邊形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{π}$ | B. | $-\sqrt{π}$ | C. | $\frac{{\sqrt{π}}}{2π}$ | D. | $\frac{{\sqrt{2π}}}{2π}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
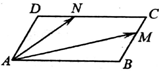 如圖,在平行四邊形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分別是邊BC、CD上的點,且滿足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],則$\overrightarrow{AM}•\overrightarrow{AN}$的取值范圍是( )
如圖,在平行四邊形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分別是邊BC、CD上的點,且滿足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],則$\overrightarrow{AM}•\overrightarrow{AN}$的取值范圍是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2,1) | B. | (-2,1] | C. | [-3,3) | D. | (-3,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com