Question

【題目】在如圖所示的幾何體中，底面ABCD中，AB⊥AD，AD＝2，AB＝3，BC＝BE＝7，△DCE是邊長為6的正三角形．

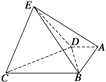
(1)求證：平面DEC⊥平面BDE；

(2)求點A到平面BDE的距離．

Answer 1

【答案】（1）見解析；（2）．

【解析】試題分析：（1）由勾股定理及逆定理可得，從而有線面垂直，于是可得面面垂直；

（2）到平面的距離可用體積法求得， ．

試題解析：

(1)證明　因為AB⊥AD，AD＝2，AB＝3，所以BD＝，

又因為BC＝7，CD＝6，所以根據勾股定理可得BD⊥CD，

因為BE＝7，DE＝6，同理可得BD⊥DE．

因為DE∩CD＝D，DE平面DEC，CD平面DEC，

所以BD⊥平面DEC．因為BD平面BDE，

所以平面DEC⊥平面BDE．

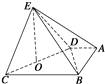
(2)解　如圖，取CD的中點O，連接OE，

因為△DCE是邊長為6的正三角形，

所以EO⊥CD，EO＝3，

易知EO⊥平面ABCD，

則VE－ABD＝××2×3×3＝3，

又因為直角三角形BDE的面積為×6×＝3，

設點A到平面BDE的距離為h，則由VE－ABD＝VA－BDE，

得×3h＝3，所以h＝，所以點A到平面BDE的距離為．