
【題目】已知函數![]() ,且
,且![]() .
.
(1)求函數![]() 在
在![]() 上的單調區間,并給以證明;
上的單調區間,并給以證明;
(2)設關于![]() 的方程
的方程![]() 的兩根為
的兩根為![]() ,試問是否存在實數
,試問是否存在實數![]() ,使得不等式
,使得不等式![]() 對任意的
對任意的![]() 及
及![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)單調遞增區間為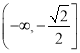 ,單調遞減區間為
,單調遞減區間為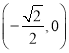 ;
;
(2)存在實數![]() 符合題意,其取值范圍是
符合題意,其取值范圍是![]() .
.
【解析】試題分析:(1)由![]() 可得
可得![]() ,所以
,所以![]() ,然后利用函數單調性的定義求出函數
,然后利用函數單調性的定義求出函數![]() 在
在![]() 上的單調遞增區間為
上的單調遞增區間為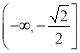 ,單調遞減區間為
,單調遞減區間為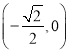 。(2)由題意先求出
。(2)由題意先求出![]() 的最大值為3,所以由題意可得當
的最大值為3,所以由題意可得當![]() ,不等式
,不等式![]() 恒成立,構造函數
恒成立,構造函數![]() ,只需滿足
,只需滿足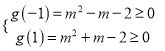 ,解得
,解得![]() 或
或![]() ,由此可得所求范圍,從而說明存在實數
,由此可得所求范圍,從而說明存在實數![]() 滿足題意。
滿足題意。
試題解析:
(1)∵![]() ,
,
∴![]() ,
,
∴![]() 。
。
設![]() ,且
,且![]() ,
,
則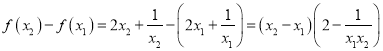 ,
,
①當![]() 時,
時, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴函數![]() 在
在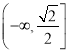 上單調遞增;
上單調遞增;
②當![]() 時,
時, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴函數![]() 在
在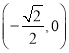 上單調遞減,
上單調遞減,
∴函數![]() 在
在![]() 上的單調遞增區間為
上的單調遞增區間為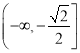 ,單調遞減區間為
,單調遞減區間為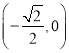 ;
;
(2)由![]() ,得
,得![]() ,
,
∴![]() 是方程
是方程![]() 的兩根,
的兩根,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
故由題意得當![]() ,不等式
,不等式![]() 恒成立,
恒成立,
設![]() ,
,
則只須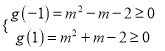 ,
,
解得![]() 或
或![]() ,
,
故存在實數![]() 符合題意,其取值范圍是
符合題意,其取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是邊長為6的正三角形.
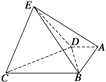
(1)求證:平面DEC⊥平面BDE;
(2)求點A到平面BDE的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙二人同時從![]() 地趕住
地趕住![]() 地,甲先騎自行車到兩地的中點再改為跑步;乙先跑步到兩地的中點再改為騎自行車,最后兩人同時到達
地,甲先騎自行車到兩地的中點再改為跑步;乙先跑步到兩地的中點再改為騎自行車,最后兩人同時到達![]() 地.已知甲騎自行車比乙騎自行車的速度快,且兩人騎車的速度均大于跑步的速度.現將兩人離開
地.已知甲騎自行車比乙騎自行車的速度快,且兩人騎車的速度均大于跑步的速度.現將兩人離開![]() 地的距離
地的距離![]() 與所用時間
與所用時間![]() 的函數關系用圖象表示如下:
的函數關系用圖象表示如下:

則上述四個函數圖象中,甲、乙兩人運行的函數關系的圖象應該分別是( )
A. 圖①、圖② B. 圖①、圖④ C. 圖③、圖② D. 圖③、圖④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一片森林原面積為![]() .計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的
.計劃從某年開始,每年砍伐一些樹林,且每年砍伐面積的百分比相等.并計劃砍伐到原面積的一半時,所用時間是10年.為保護生態環境,森林面積至少要保留原面積的![]() .已知到今年為止,森林剩余面積為原面積的
.已知到今年為止,森林剩余面積為原面積的![]() .
.
(1)求每年砍伐面積的百分比;
(2)到今年為止,該森林已砍伐了多少年?
(3)為保護生態環境,今后最多還能砍伐多少年?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,以
兩點,以![]() 為對角線作正方形
為對角線作正方形![]() ,記直線
,記直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,問
,問![]() 、
、![]() 兩點間距離是否為定值?如果是,求出定值;如果不是,請說明理由.
兩點間距離是否為定值?如果是,求出定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌汽車的![]() 店,對最近100份分期付款購車情況進行統計,統計情況如下表所示.已知分9期付款的頻率為0.4;該店經銷一輛該品牌汽車,若顧客分3期付款,其利潤為1萬元;分6期或9期付款,其利潤為2萬元;分12期付款,其利潤為3萬元.
店,對最近100份分期付款購車情況進行統計,統計情況如下表所示.已知分9期付款的頻率為0.4;該店經銷一輛該品牌汽車,若顧客分3期付款,其利潤為1萬元;分6期或9期付款,其利潤為2萬元;分12期付款,其利潤為3萬元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
頻數 | 20 | 20 |
|
|
(1)若以上表計算出的頻率近似替代概率,從該店采用分期付款購車的顧客(數量較大)中隨機抽取3為顧客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分層抽樣方式從這100為顧客中抽取5人,再從抽取的5人中隨機抽取3人,記該店在這3人身上賺取的總利潤為隨機變量![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com