已知數(shù)列

計算
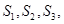
由此推測出

的計算公式,并用數(shù)學歸納法證明.
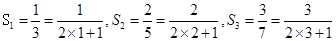
,推測

,證明過程詳見解析.
試題分析:計算

的值可以推出

,利用數(shù)學歸納法可以證明,首先驗證n=1時,結論成立,接下來假設n=k(

)時結論成立,即有
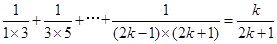
,最后只需證明n=k+1時,結論也成立,利用
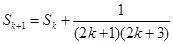
即可得證.
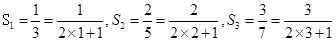
,
∴推測
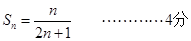
①n=1時,左邊=
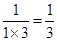
,右邊=
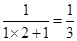
,左邊=右邊,所以等式成立 6分
②假設n=k時等式成立,即有
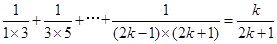
,
則當n=k+1時,
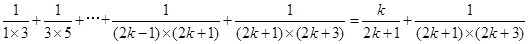

所以當n=k+1時,等式也成立 13分
由①,②可知,對一切
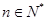
等式都成立 14分.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
用數(shù)學歸納法證明:對任意
n∈N
+,

成立.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
觀察下列不等式
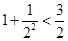
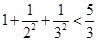
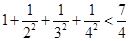
……
照此規(guī)律,第五個不等式為________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
用數(shù)學歸納法證明“n
3+(n+1)
3+(n+2)
3(n∈N
*)能被9整除”,要利用歸納假設證n=k+1時的情況,只需展開( )
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
用數(shù)學歸納法證明:


的第二步中,當

時等式左邊與

時的等式左邊的差等于
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
記
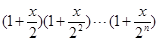
的展開式中,
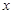
的系數(shù)為
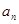
,
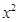
的系數(shù)為
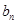
,其中
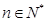
(1)求
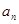
(2)是否存在常數(shù)p,q(p<q),使
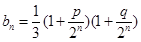
,對
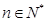
,
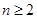
恒成立?證明你的結論.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
是否存在實數(shù)
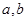
使得關于n的等式
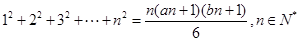
成立?若存在,求出
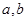
的值并證明等式,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
觀察下列等式:

;
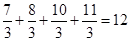
;

;……
則當

且

時,

.(最后結果用

表示)
查看答案和解析>>

 計算
計算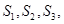 由此推測出
由此推測出 的計算公式,并用數(shù)學歸納法證明.
的計算公式,并用數(shù)學歸納法證明.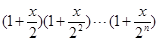 的展開式中,
的展開式中,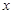 的系數(shù)為
的系數(shù)為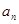 ,
,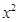 的系數(shù)為
的系數(shù)為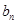 ,其中
,其中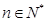
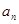 (2)是否存在常數(shù)p,q(p<q),使
(2)是否存在常數(shù)p,q(p<q),使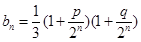 ,對
,對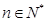 ,
,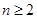 恒成立?證明你的結論.
恒成立?證明你的結論.