
分析 進行數量積的運算,先求出$\overrightarrow{a}•\overrightarrow{b}=m$,$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{\frac{5{m}^{2}}{4}-2m+\frac{5}{4}}$,并且容易判斷函數f(x)為偶函數,且單調遞增在(0,+∞)上,從而根據$f(\overrightarrow{a}•\overrightarrow{b})≥f(|\overrightarrow{a}-\overrightarrow{b}|)$便可得到不等式$m≥\sqrt{\frac{5}{4}{m}^{2}-2m+\frac{5}{4}}$,這樣解該不等式便可得出m的取值范圍.
解答 解:∵$\overrightarrow a=(m,1),\overrightarrow b=(\frac{1}{2},\frac{m}{2})$,m>0;
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{m}{2}+\frac{m}{2}=m$,$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{(m-\frac{1}{2})^{2}+(1-\frac{m}{2})^{2}}$=$\sqrt{\frac{5{m}^{2}}{4}-2m+\frac{5}{4}}$;
由$f(x)={log_2}({x^2}+2)$知f(x)為偶函數且在(0,+∞)上單調遞增;
∵$f(\overrightarrow a•\overrightarrow b)≥f(|\overrightarrow a-\overrightarrow b|)$;
∴$\overrightarrow a•\overrightarrow b≥|\overrightarrow a-\overrightarrow b|$;
∴$m≥\sqrt{\frac{5}{4}{m^2}-2m+\frac{5}{4}}$且m>0;
∴解得$4-\sqrt{11}≤m≤4+\sqrt{11}$;
∴m的取值范圍為$[4-\sqrt{11},4+\sqrt{11}]$.
點評 考查數量積的坐標運算,向量坐標的減法運算,以及偶函數和增函數的定義及判斷,無理不等式的解法.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 最小值4 | B. | 最大值4 | C. | 最小值2 | D. | 最大值2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
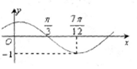 函數f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的圖象如圖所示,為了得到g(x)=sinωx的圖象,則只要將f(x)的圖象( )
函數f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的圖象如圖所示,為了得到g(x)=sinωx的圖象,則只要將f(x)的圖象( )| A. | 向左平移$\frac{π}{3}$個單位長度 | B. | 向右平移$\frac{π}{3}$個單位長度 | ||
| C. | 向右平移$\frac{π}{6}$個單位長度 | D. | 向左平移$\frac{π}{6}$個單位長度 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{81}{22}$ | B. | $\frac{1}{3}$ | C. | 5 | D. | .4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com