
分析 由題意可知函數(shù)一定為二次函數(shù)即a≠0,圖象關(guān)于y軸對(duì)稱可判斷出b=0,即函數(shù)解析式化簡成f(x)=ax2+3a,由定義域[a-1,2a]關(guān)于y軸對(duì)稱,得出a的值,求函數(shù)f(x)的單調(diào)減區(qū)間.
解答 解:由題意可知函數(shù)一定為二次函數(shù)即a≠0,而圖象關(guān)于y軸對(duì)稱可判斷出b=0,即函數(shù)解析式化簡成f(x)=ax2+3a.
由定義域[a-1,2a]關(guān)于y軸對(duì)稱,故有a-1+2a=0,得出a=$\frac{1}{3}$,即函數(shù)解析式化簡成f(x)=$\frac{1}{3}$x2+1,x∈[-$\frac{2}{3}$,$\frac{2}{3}$].
二次函數(shù)的開口向上,函數(shù)f(x)的單調(diào)減區(qū)間為:[$-\frac{2}{3}$,0].
故答案為:[$-\frac{2}{3}$,0].(端點(diǎn)在不在都可以).
點(diǎn)評(píng) 此題主要考查函數(shù)二次函數(shù)圖象對(duì)稱的性質(zhì)以及二次函數(shù)的值域的求法,求解的關(guān)鍵是熟練掌握二次函數(shù)的性質(zhì),本題理解對(duì)稱性很關(guān)鍵.


 激活思維優(yōu)加課堂系列答案
激活思維優(yōu)加課堂系列答案 活力試卷系列答案
活力試卷系列答案 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=2x | B. | y=x2 | C. | y=log2x | D. | y=sin2x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{\sqrt{5}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
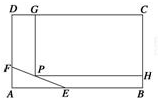 如圖所示,為了保護(hù)環(huán)境,實(shí)現(xiàn)城市綠化,某房地產(chǎn)公司要在拆遷地長方形ABCD處規(guī)劃一塊長方形地面HPGC,建造住宅小區(qū)公園,但不能越過文物保護(hù)區(qū)三角形AEF的邊線EF.已知AB=CD=200m,BC=AD=160m,AF=40m,AE=60m,問如何設(shè)計(jì)才能使公園占地面積最大,求出最大面積.
如圖所示,為了保護(hù)環(huán)境,實(shí)現(xiàn)城市綠化,某房地產(chǎn)公司要在拆遷地長方形ABCD處規(guī)劃一塊長方形地面HPGC,建造住宅小區(qū)公園,但不能越過文物保護(hù)區(qū)三角形AEF的邊線EF.已知AB=CD=200m,BC=AD=160m,AF=40m,AE=60m,問如何設(shè)計(jì)才能使公園占地面積最大,求出最大面積.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
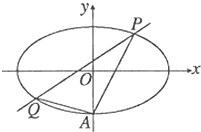 設(shè)橢圓E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)過A(0,-1),焦點(diǎn)為F1,F(xiàn)2,橢圓E上滿足MF1⊥MF2的點(diǎn)M有且僅有兩個(gè).
設(shè)橢圓E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)過A(0,-1),焦點(diǎn)為F1,F(xiàn)2,橢圓E上滿足MF1⊥MF2的點(diǎn)M有且僅有兩個(gè).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
 在三棱錐P-ABC中,底面ABC為直角三角形,AB=BC,PA⊥平面ABC.
在三棱錐P-ABC中,底面ABC為直角三角形,AB=BC,PA⊥平面ABC.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com