
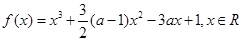 .
. 的單調區間;
的單調區間;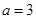 時,若函數
時,若函數 在區間
在區間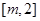 上的最大值為28,求
上的最大值為28,求 的取值范圍.
的取值范圍.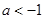 時,
時, 在
在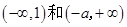 內單調遞增,
內單調遞增, 在
在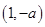 內單調遞減;當
內單調遞減;當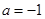 時,
時, 在
在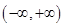 單調遞增;當
單調遞增;當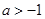 時,
時, 在
在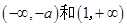 內單調遞增,
內單調遞增, 在
在 內單調遞減;(Ⅱ)即
內單調遞減;(Ⅱ)即 的取值范圍是
的取值范圍是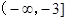 .
. 的單調區間,它的解題方法有兩種:一是利用定義,二是導數法,本題由于是三次函數,可用導數法求單調區間,只需求出
的單調區間,它的解題方法有兩種:一是利用定義,二是導數法,本題由于是三次函數,可用導數法求單調區間,只需求出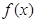 的導函數,判斷
的導函數,判斷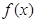 的導函數的符號,從而求出
的導函數的符號,從而求出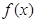 的單調區間;但本題求導后令
的單調區間;但本題求導后令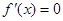 ,得
,得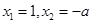 ,由于不知
,由于不知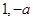 的大小,因此需要對
的大小,因此需要對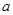 進行分類討論,從而確定在各種情況下的單調區間;(Ⅱ)當
進行分類討論,從而確定在各種情況下的單調區間;(Ⅱ)當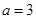 時,若函數
時,若函數 在區間
在區間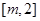 上的最大值為28,求
上的最大值為28,求 的取值范圍,這是函數在閉區間上的最值問題,像這一類問題的處理方法為,先求出
的取值范圍,這是函數在閉區間上的最值問題,像這一類問題的處理方法為,先求出 的極值點,然后分別求出極值點與區間端點處的函數值,比較誰大誰為最大值,比較誰小誰為最小值,但本題是給出最大值,確定區間端點的取值范圍,只需找出包含最大值28的
的極值點,然后分別求出極值點與區間端點處的函數值,比較誰大誰為最大值,比較誰小誰為最小值,但本題是給出最大值,確定區間端點的取值范圍,只需找出包含最大值28的 的取值范圍,
的取值范圍,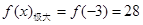 ,故故區間
,故故區間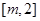 內必須含有
內必須含有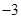 ,即
,即 的取值范圍是
的取值范圍是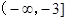 .
.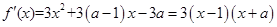 ,令
,令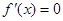 得
得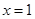 ,
,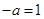 ,即
,即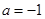 時,
時, ,
, 在
在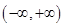 單調遞增,
單調遞增,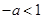 ,即
,即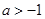 時,當
時,當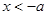 ,或
,或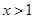 時,
時,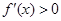 ,
, 在
在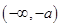 、
、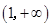 內單調遞增,當
內單調遞增,當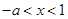 時
時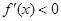 ,
, 在
在 內單調遞減,
內單調遞減,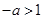 ,即
,即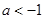 時,當
時,當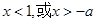 時
時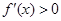 ,
, 在
在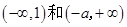 內單調遞增
內單調遞增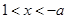 時
時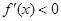 ,
, 在
在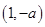 內單調遞減 ,
內單調遞減 ,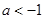 時,
時, 在
在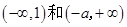 內單調遞增,
內單調遞增, 在
在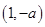 內單調遞減;當
內單調遞減;當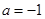 時,
時, 在
在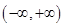 單調遞增;當
單調遞增;當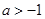 時,
時, 在
在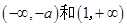 內單調遞增,
內單調遞增, 在
在 內單調遞減;
內單調遞減;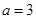 時,
時,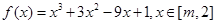 ,
,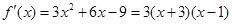 ,令
,令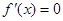 得
得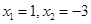 ,將
,將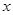 ,
,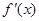 ,
, 變化情況列表如下:
變化情況列表如下: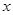 | 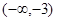 | 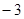 | 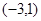 | 1 | 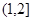 |
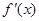 | 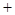 | 0 |  | 0 |  |
 | ↗ | 極大 | ↘ | 極小 | ↗ |
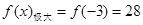 ,
,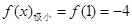 ,
,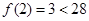 ,故區間
,故區間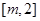 內必須含有
內必須含有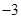 ,即
,即 的取值范圍是
的取值范圍是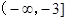 .
.

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com