
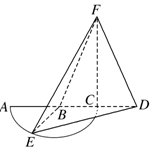
 如圖,以AC=2為直徑的⊙B,點E為$\widehat{AC}$的中點,點D在直徑AC延長線上,CD=1,FC⊥平面BED,FC=2.
如圖,以AC=2為直徑的⊙B,點E為$\widehat{AC}$的中點,點D在直徑AC延長線上,CD=1,FC⊥平面BED,FC=2.分析 (Ⅰ)證明:EB⊥平面FBD,即可證明EB⊥FD;
(Ⅱ)在平面FCH內過C作CK⊥FH,則CK⊥平面FED.即可求點B到平面FED的距離.
解答 (Ⅰ)證明:∵FC⊥平面BED,BE?平面BED,∴EB⊥FC.
又點E為$\widehat{AC}$的中點,B為直徑AC的中點,∴EB⊥BC.
又∵FC∩BC=C,∴EB⊥平面FBD.
∵FD?平面FBD,∴EB⊥FD.
(Ⅱ)解:如圖,在平面BEC內過C作CH⊥ED,連接FH.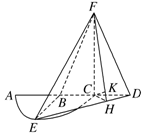
則由FC⊥平面BED知,ED⊥平面FCH.
∵Rt△DHC∽Rt△DBE,∴$\frac{DC}{DE}$=$\frac{CH}{BE}$.
在Rt△DBE中,DE=$\sqrt{B{E}^{2}+B{D}^{2}}$=$\sqrt{5}$,
∴CH=$\frac{DC•BE}{DE}$=$\frac{\sqrt{5}}{5}$.
在平面FCH內過C作CK⊥FH,則CK⊥平面FED.
∵FC=2.∴FH2=FC2+CH2=$\frac{21}{5}$,∴FH=$\frac{\sqrt{105}}{5}$.
∴CK=$\frac{FC•CH}{FH}$=$\frac{2\sqrt{21}}{21}$.
∵C是BD的中點,∴B到平面FED的距離為2CK=$\frac{4\sqrt{21}}{21}$.
點評 本題考查線面平行的判定與性質,考查點到平面距離的計算,屬于中檔題.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{8}$ | B. | $\frac{5}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{14}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
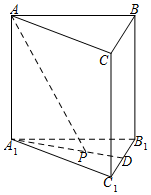 已知正三棱柱(底面是正三角形,且側棱與底面垂直的棱柱)ABC-A1B1C1體積為$\frac{9}{4}$,底面邊長為$\sqrt{3}$.若P為底面A1B1C1的中心,則PA與平面ABC所成角的大小為( )
已知正三棱柱(底面是正三角形,且側棱與底面垂直的棱柱)ABC-A1B1C1體積為$\frac{9}{4}$,底面邊長為$\sqrt{3}$.若P為底面A1B1C1的中心,則PA與平面ABC所成角的大小為( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | e2e+3f(e)<e2ππ3f(π) | B. | e2e+3f(π)>e2ππ3f(e) | C. | e2e+3f(π)<e2ππ3f(e) | D. | e2e+3f(e)>e2ππ3f(π) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | -1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com