
分析 (1)由題意可得f(-1)=0,判別式為0,解方程可得a=1,b=2,進而得到函數的解析式;
(2)①根據二次函數的性質即可求出k的范圍.
②需要分類討論,根據二次函數的性質即可求出k的值.
解答 解:(1)由題意得:$\left\{\begin{array}{l}a-b+1=0\\ \frac{{4a-{b^2}}}{4a}=0\end{array}\right.$,得$\left\{\begin{array}{l}a=1\\ b=2\end{array}\right.$,
所以f(x)=x2+2x+1,
(2)①g(x)=x2-2(k-1)x+1;
所以k-1≤-2或k-1≥2,即k≤-1或k≥3;
②當k-1≤-2即k≤-1時,g(x)min=g(-2)=4k+1=-15,得k=-4;
當k-1≥2即k≥3時,g(x)min=g(2)=9-4k=-15,得k=6;
當-2<k-1<2即-1<k<3時,$g{(x)_{min}}=g(k-1)=1-{(k-1)^2}=-15$,得k=-3(舍)或k=5(舍)
綜上k=-4或k=6.
點評 本題考查函數的解析式的求法,注意運用二次函數的值域,考查函數的單調性的運用,屬于中檔題


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $2\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
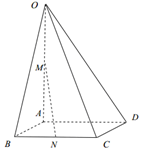 如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.
如圖,在四棱錐O-ABCD中,底面ABCD是四邊長為$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M為OA的中點,N為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=-x2+2x+3,x∈[-1,2)
已知函數f(x)=-x2+2x+3,x∈[-1,2)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com