
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②③④ |
分析 根據向量的運算性質分別判斷即可.
解答 解:對于①$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$,錯誤,應是$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$;
②$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}$,正確;
③若($\overrightarrow{AB}+\overrightarrow{AC})•(\overrightarrow{AB}-\overrightarrow{AC})=0$•($\overrightarrow{AB}-\overrightarrow{AC})$=0,則${\overrightarrow{AB}}^{2}$-${\overrightarrow{AC}}^{2}$=0,
∴|$\overrightarrow{AB}$|2=|$\overrightarrow{AC}$|2,故AB=AC,
△ABC為等腰三角形,故③正確;
④若$\overrightarrow{AB}•\overrightarrow{AC}>0$,則△ABC不一定是銳角三角形,
故④錯誤;
故選:C.
點評 本小題主要考查向量的數量積、向量的模、向量在幾何中的應用等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.


科目:高中數學 來源: 題型:解答題
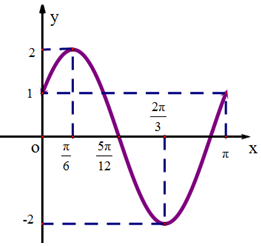 已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示.
已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a2>b2,則a>b | B. | 若ac>bc,則a>b | C. | 若$\frac{1}{a}>\frac{1}{b},則a<b$ | D. | 若$\sqrt{a}<\sqrt{b},則a<b$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知平面ABC⊥平面BCDE,△DEF與△ABC分別是棱長為1與2的正三角形,AC∥DF,四邊形BCDE為直角梯形,DE∥BC,BC⊥CD,CD=1,點G為△ABC的重心,N為AB中點,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如圖,已知平面ABC⊥平面BCDE,△DEF與△ABC分別是棱長為1與2的正三角形,AC∥DF,四邊形BCDE為直角梯形,DE∥BC,BC⊥CD,CD=1,點G為△ABC的重心,N為AB中點,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | enf(-n)<f(0),f(n)>enf(0) | B. | enf(-n)<f(0),f(n)<enf(0) | ||
| C. | enf(-n)>f(0),f(n)>enf(0) | D. | enf(-n)>f(0),f(n)<enf(0) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com