
分析 由題意畫出圖形,求出A的坐標,結(jié)合向量等式求得C的坐標,代入橢圓方程可解e的值.
解答 解:如圖,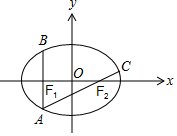
由題意,A(-c,$-\frac{{b}^{2}}{a}$),
∵$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}C}$,∴${y}_{C}=\frac{{b}^{2}}{2a}$,且xC-c=c,得xC=2c.
∴C(2c,$\frac{{b}^{2}}{2a}$),代入橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,
得$\frac{4{c}^{2}}{{a}^{2}}+\frac{{b}^{2}}{4{a}^{2}}=1$,即5c2=a2,解得e=$\frac{\sqrt{5}}{5}$.
故答案為:$\frac{{\sqrt{5}}}{5}$.
點評 本題考查橢圓的簡單性質(zhì),考查了平面向量在求解圓錐曲線問題中的應用,是中檔題.


科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
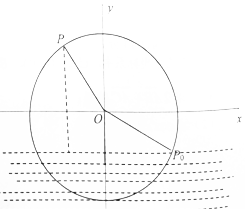 一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉(zhuǎn)動5圈,如果當水輪上點P從水中浮現(xiàn)時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數(shù):f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半徑為4米的水輪如圖所示,水輪圓心O距離水面2米,已知水輪每60秒逆時針轉(zhuǎn)動5圈,如果當水輪上點P從水中浮現(xiàn)時(圖象P0點)開始計算時間,且點P距離水面的高度f(t)(米)與時間t(秒)滿足函數(shù):f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
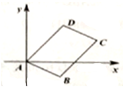 如圖,面積為8的平行四邊形ABCD,A為坐標原點,B坐標為(2,-1),C、D均在第一象限.
如圖,面積為8的平行四邊形ABCD,A為坐標原點,B坐標為(2,-1),C、D均在第一象限.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com