
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,分別過
有且僅有一個公共點,分別過![]() 兩點作
兩點作![]() ,垂足分別為
,垂足分別為![]() ,且記
,且記![]() 為點
為點![]() 到直線
到直線![]() 的距離,
的距離, ![]() 為點
為點![]() 到直線
到直線![]() 的距離,
的距離,![]() 為點
為點![]() 到點
到點![]() 的距離,試探索
的距離,試探索![]() 是否存在最大值.若存在,求出最大值;若不存在,請說明理由.
是否存在最大值.若存在,求出最大值;若不存在,請說明理由.
 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)=sin(wx+![]() )(w>0,
)(w>0,![]() <
<![]() )的最小正周期是π,若將該函數的圖象向右平移
)的最小正周期是π,若將該函數的圖象向右平移![]() 個單位后得到的函數圖象關于直線x=
個單位后得到的函數圖象關于直線x=![]() 對稱,則函數f(x)的解析式為( )
對稱,則函數f(x)的解析式為( )
A.f(x)=sin(2x+![]() )B.f(x)=sin(2x-
)B.f(x)=sin(2x-![]() )
)
C.f(x)=sin(2x+![]() )D.f(x)=sin(2x-
)D.f(x)=sin(2x-![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且與
且與![]() 軸不重合,交圓
軸不重合,交圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
(1)求![]() 的值;
的值;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,與直線
兩點,與直線![]() 相交于
相交于![]() 點,試問在橢圓
點,試問在橢圓![]() 上是否存在一定點
上是否存在一定點![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差數列(其中
成等差數列(其中![]() ,
,![]() ,
,![]() 分別指直線
分別指直線![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與
與![]() ,
,![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() ,若點
,若點![]() 在曲線
在曲線![]() 位于第一象限的圖象上運動,求四邊形
位于第一象限的圖象上運動,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位鼓勵員工參加健身運動,推廣了一款手機軟件,記錄每人每天走路消耗的卡路里;軟件的測評人員從員工中隨機地選取了40人(男女各20人),記錄他們某一天消耗的卡路里,并將數據整理如下:
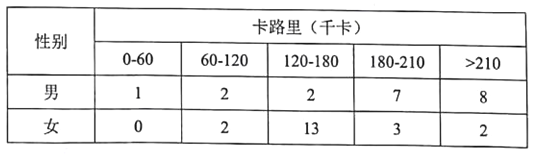
(1)已知某人一天的走路消耗卡路里超過180千卡被評測為“積極型”,否則為“懈怠型”,根據題中數據完成下面的![]() 列聯表,并據此判斷能否有99%以上把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有99%以上把握認為“評定類型”與“性別”有關?
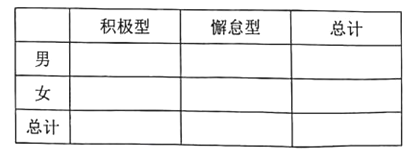
(2)若測評人員以這40位員工每日走路所消耗的卡路里的頻率分布來估計其所有員工每日走路消耗卡路里的頻率分布,現在測評人員從所有員工中任選2人,其中每日走路消耗卡路里不超過120千卡的有![]() 人,超過210千卡的有
人,超過210千卡的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附: 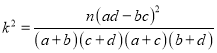 ,其中
,其中![]() .
.
參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是劉徽最突出的數學成就之一,他在《九章算術注》中提出割圓術,并作為計算圓的周長,面積已經圓周率的基礎,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數值,這個結果是當時世界上圓周率計算的最精確數據.如圖,當分割到圓內接正六邊形時,某同學利用計算機隨機模擬法向圓內隨機投擲點,計算得出該點落在正六邊形內的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數據:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)試討論函數![]() 的極值點的個數;
的極值點的個數;
(2)若![]() ,且
,且![]() 恒成立,求a的最大值.
恒成立,求a的最大值.
參考數據:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.588 | 2.303 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健身館為響應十九屆四中全會提出的“聚焦增強人民體質,健全促進全民健身制度性舉措”,提高廣大市民對全民健身運動的參與程度,推出了讓健身館會員參與的健身促銷活動.
(1)為了解會員對促銷活動的興趣程度,現從某周六參加該健身館健身活動的會員中隨機采訪男性會員和女性會員各![]() 人,他們對于此次健身館健身促銷活動感興趣的程度如下表所示:
人,他們對于此次健身館健身促銷活動感興趣的程度如下表所示:
感興趣 | 無所謂 | 合計 | |
男性 |
|
|
|
女性 |
|
|
|
合計 |
|
|
|
根據以上數據能否有![]() 的把握認為“對健身促銷活動感興趣”與“性別”有關?
的把握認為“對健身促銷活動感興趣”與“性別”有關?
(參考公式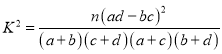 ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
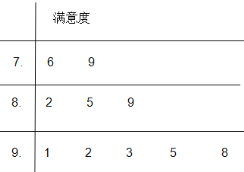
(2)在感興趣的會員中隨機抽取![]() 人對此次健身促銷活動的滿意度進行調查,以莖葉圖記錄了他們對此次健身促銷活動滿意度的分數(滿分
人對此次健身促銷活動的滿意度進行調查,以莖葉圖記錄了他們對此次健身促銷活動滿意度的分數(滿分![]() 分),如圖所示,若將此莖葉圖中滿意度分為“很滿意”(分數不低于
分),如圖所示,若將此莖葉圖中滿意度分為“很滿意”(分數不低于![]() 分)、“滿意”(分數不低于平均分且低于
分)、“滿意”(分數不低于平均分且低于![]() 分)、“基本滿意”(分數低于平均分)三個級別.先從“滿意”和“很滿意”的會員中隨機抽取兩人參加回訪饋贈活動,求這兩人中至少有一人是“很滿意”會員的概率.
分)、“基本滿意”(分數低于平均分)三個級別.先從“滿意”和“很滿意”的會員中隨機抽取兩人參加回訪饋贈活動,求這兩人中至少有一人是“很滿意”會員的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com