
【題目】已知![]() 的三個頂點都在橢圓C:
的三個頂點都在橢圓C:![]() 上,且
上,且![]() 過橢圓的左焦點F,O為坐標原點,M在
過橢圓的左焦點F,O為坐標原點,M在![]() 上,且
上,且![]() .
.
(1)求點M的軌跡方程;
(2)求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)
【解析】
(1)法一(代數法)設![]() :
:![]() ,
,![]() ,聯立方程組,消去m得
,聯立方程組,消去m得![]() ,即可推出結果.
,即可推出結果.
法二(幾何法)由已知可得![]() ,
,![]() ,說明M的軌跡為以
,說明M的軌跡為以![]() 為直徑的圓(經檢驗,原點也符合題意).求解即可.
為直徑的圓(經檢驗,原點也符合題意).求解即可.
(2)由(1)知,M的軌跡為以![]() 為圓心,1為半徑的圓,設
為圓心,1為半徑的圓,設![]() ,則
,則![]() ,求出
,求出![]() 的表達式,利用二次函數的性質求解最大值與最小值即可.
的表達式,利用二次函數的性質求解最大值與最小值即可.
(1)法一(代數法)
由已知可得![]() ,故當直線
,故當直線![]() 斜率不為0時,可設
斜率不為0時,可設![]() :
:![]() ,
,![]()
由![]() 消去m得
消去m得![]() (
(![]() )
)
經檢驗,當直線![]() 斜率為0,即m存在時,
斜率為0,即m存在時,![]() 也符合上式,
也符合上式,
故點M的軌跡方程為:![]() .
.
法二(幾何法)
由已知可得![]() ,
,![]() ,
,
所以M的軌跡為以![]() 為直徑的圓(經檢驗,原點也符合題意),
為直徑的圓(經檢驗,原點也符合題意),
∴M的軌跡方程為:![]() .
.
(2)由(1)知,M的軌跡為以![]() 為圓心,1為半徑的圓,設
為圓心,1為半徑的圓,設![]()
則![]() (
(![]() ),
),
可得 ,
,
當![]() 時,
時,
當![]() 時,
時,![]() ,
,
所以![]() 的取值范圍是
的取值范圍是 .
.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,沿
的中點,沿![]() 將
將![]() 折起,使得點
折起,使得點![]() 到點
到點![]() 位置,且
位置,且![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 上的動點(與點
上的動點(與點![]() ,
,![]() 不重合).
不重合).
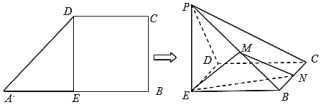
(Ⅰ)證明:平面![]() 平面
平面![]() 垂直;
垂直;
(Ⅱ)是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值
的余弦值![]() ?若存在,確定
?若存在,確定![]() 點位置;若不存在,說明理由.
點位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】維生素C又叫抗壞血酸,是一種水溶性維生素,是高等靈長類動物與其他少數生物的必需營養素.維生素C雖不直接構成腦組織,也不向腦提供活動能源,但維生素C有多種健腦強身的功效,它是腦功能極為重要的營養物.維生素C的毒性很小,但食用過多仍可產生一些不良反應.根據食物中維C的含量可大致分為:含量很豐富:鮮棗、沙棘、獼猴桃、柚子,每100克中的維生素C含量超過100毫克;比較豐富:青椒、桂圓、番茄、草莓、甘藍、黃瓜、柑橘、菜花,每100克中維生素C含量超過50毫克;相對豐富:白菜、油菜、香菜、菠菜、芹菜、莧菜、菜苔、豌豆、豇豆、蘿卜,每100克中維生素C含量超過30~50毫克.現從獼猴桃、柚子兩種食物中測得每100克所含維生素C的量(單位:![]() )得到莖葉圖如圖所示,則下列說法中不正確的是( )
)得到莖葉圖如圖所示,則下列說法中不正確的是( )
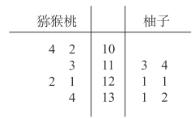
A.獼猴桃的平均數小于柚子的平均數
B.獼猴桃的方差小于柚子的方差
C.獼猴桃的極差為32
D.柚子的中位數為121
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來隨著我國在教育科研上的投入不斷加大,科學技術得到迅猛發展,國內企業的國際競爭力得到大幅提升.伴隨著國內市場增速放緩,國內有實力企業紛紛進行海外布局,第二輪企業出海潮到來.如在智能手機行業,國產品牌已在趕超國外巨頭,某品牌手機公司一直默默拓展海外市場,在海外共設30多個分支機構,需要國內公司外派大量80后、90后中青年員工.該企業為了解這兩個年齡層員工是否愿意被外派工作的態度,按分層抽樣的方式從80后和90后的員工中隨機調查了100位,得到數據如下表:
愿意被外派 | 不愿意被外派 | 合計 | |
80后 | 20 | 20 | 40 |
90后 | 40 | 20 | 60 |
合計 | 60 | 40 | 100 |
(1)根據調查的數據,是否有99%的把握認為“是否愿意被外派與年齡有關”,并說明理由;
(2)該公司舉行參觀駐海外分支機構的交流體驗活動,擬安排6名參與調查的80后、90后員工參加.80后員工中有愿意被外派的3人和不愿意被外派的3人報名參加,從中隨機選出3人,記選到愿意被外派的人數為![]() ;90后員工中有愿意被外派的4人和不愿意被外派的2人報名參加,從中隨機選出3人,記選到愿意被外派的人數為
;90后員工中有愿意被外派的4人和不愿意被外派的2人報名參加,從中隨機選出3人,記選到愿意被外派的人數為![]() ,求
,求![]() 的概率.
的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(參考公式: ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,分別過
有且僅有一個公共點,分別過![]() 兩點作
兩點作![]() ,垂足分別為
,垂足分別為![]() ,且記
,且記![]() 為點
為點![]() 到直線
到直線![]() 的距離,
的距離, ![]() 為點
為點![]() 到直線
到直線![]() 的距離,
的距離,![]() 為點
為點![]() 到點
到點![]() 的距離,試探索
的距離,試探索![]() 是否存在最大值.若存在,求出最大值;若不存在,請說明理由.
是否存在最大值.若存在,求出最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線的參數方程為
,直線的參數方程為![]() ,(
,(![]() 為參數).直線
為參數).直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程.
的普通方程.
(2)設![]() ,若
,若![]() 成等比數列,求
成等比數列,求![]() 和的
和的![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 的焦點,點
的焦點,點![]() 在
在![]() 軸上,
軸上,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,經過點
,經過點![]() 且垂直于
且垂直于![]() 軸的直線與拋物線
軸的直線與拋物線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 到直線
到直線![]() 的最大距離.
的最大距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com