
| π |
| 3 |
| π |
| 3 |
A、f(x)的圖象可以由g(x)的圖象向左平移
| ||
B、f(x)的圖象可以由g(x)的圖象向右平移
| ||
C、f(x)的圖象可以由g(x)的圖象關(guān)于直線x=
| ||
D、f(x)的圖象可以由g(x)的圖象關(guān)于直線x=
|
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
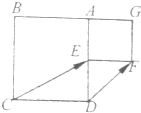 如圖,已知正方形ABCD的邊長(zhǎng)為2,點(diǎn)E為邊AD的中點(diǎn),以AE為邊向外作正方形AEFG,現(xiàn)將正方形AEFG繞點(diǎn)A按順時(shí)針?lè)较蜣D(zhuǎn)動(dòng)至AE與AB重合,則
如圖,已知正方形ABCD的邊長(zhǎng)為2,點(diǎn)E為邊AD的中點(diǎn),以AE為邊向外作正方形AEFG,現(xiàn)將正方形AEFG繞點(diǎn)A按順時(shí)針?lè)较蜣D(zhuǎn)動(dòng)至AE與AB重合,則| CE |
| DF |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| a |
| x |
| A、命題“p或q”是假命題 |
| B、命題“(¬p)且q”是真命題 |
| C、命題“p或(¬q)”是真命題 |
| D、命題“(¬p)且(¬q)”是真命題 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 21 |
| 1 |
| tanA |
| 1 |
| tanC |
| 5 |
| 4 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com