
【題目】已知橢圓C:![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,橢圓C上的一點P到
,橢圓C上的一點P到![]() ,
,![]() 的距離之和等于4.
的距離之和等于4.
(1)求橢圓C的標準方程;
(2)設![]() ,過橢圓C的右焦點
,過橢圓C的右焦點![]() 的直線與橢圓C交于A,B兩點,若滿足
的直線與橢圓C交于A,B兩點,若滿足![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
【答案】(1)![]() (2)5
(2)5
【解析】
(1)利用橢圓的定義以及離心率求出![]() ,進而可寫出橢圓的方程.
,進而可寫出橢圓的方程.
(2)由(1)可知![]() ,設
,設![]() ,
,![]() ,利用向量數量積的坐標運算可得
,利用向量數量積的坐標運算可得![]() ,分類討論設出直線方程,當直線l與x軸垂直或直線l不與x軸垂直時,將直線與橢圓聯立,利用韋達定理可將
,分類討論設出直線方程,當直線l與x軸垂直或直線l不與x軸垂直時,將直線與橢圓聯立,利用韋達定理可將![]() 用
用![]() 的式子表示,然后再利用函數的單調性即可求解.
的式子表示,然后再利用函數的單調性即可求解.
解:(1)設橢圓的焦距為![]() ,
,
由題意可得,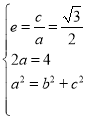 ,解得
,解得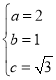 ,
,
∴橢圓C的標準方程為:![]() ;
;
(2)由(1)可知![]() ,
,
設![]() ,
,![]() ,則
,則
![]() ,
,![]() ,
,
![]() ,
,
①當直線l與x軸垂直時,直線l的方程為![]() ,得
,得![]() ,
,
代入得![]() ,
,![]() ,或
,或![]() ,
,![]() ,則
,則![]() ,
,
②當直線l不與x軸垂直時,設直線的方程為![]() ,
,
聯立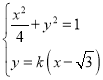 ,得
,得![]() ,
,
由韋達定理得![]() ,
,![]() ,
,
![]() ,
,
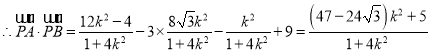
令![]() ,
,![]() ,則
,則![]() ,
,
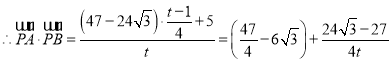 ,
,
又因函數![]() 在
在![]() 上是減函數,
上是減函數,
![]() ,
,
綜上:m的最小值為5.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】由我國引領的5G時代已經到來,5G的發展將直接帶動包括運營、制造、服務在內的通信行業整體的快速發展,進而對![]() 增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
增長產生直接貢獻,并通過產業間的關聯效應和波及效應,間接帶動國民經濟各行業的發展,創造岀更多的經濟增加值.如圖是某單位結合近年數據,對今后幾年的5G經濟產出所做的預測.結合下圖,下列說法正確的是( )
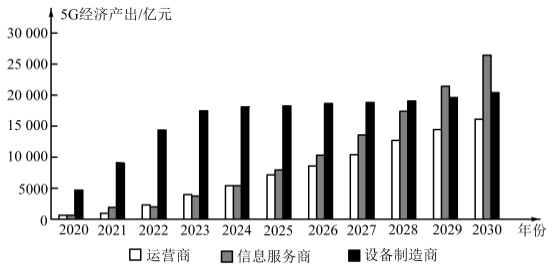
A.5G的發展帶動今后幾年的總經濟產出逐年增加
B.設備制造商的經濟產出前期增長較快,后期放緩
C.設備制造商在各年的總經濟產出中一直處于領先地位
D.信息服務商與運營商的經濟產出的差距有逐步拉大的趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)求實數![]() 的值,使得
的值,使得![]() 為奇函數;
為奇函數;
(2)若關于![]() 的方程
的方程![]() 有兩個不同實數解,求
有兩個不同實數解,求![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對由![]() 和
和![]() 這兩個數字組成的字符串,作如下規定:按從左向右的順序,當第一個子串“
這兩個數字組成的字符串,作如下規定:按從左向右的順序,當第一個子串“![]() ”的最后一個
”的最后一個![]() 所在數位是第
所在數位是第![]() (
(![]() ,且
,且![]() )位,則稱子串“
)位,則稱子串“![]() ”在第
”在第![]() 位出現;再繼續從第
位出現;再繼續從第![]() 位按從左往右的順序找子串“
位按從左往右的順序找子串“![]() ”,若第二個子串“
”,若第二個子串“![]() ”的最后一個
”的最后一個![]() 所在數位是第
所在數位是第![]() 位(其中
位(其中![]() 且
且![]() ),則稱子串“
),則稱子串“![]() ”在第
”在第![]() 位出現;……;如此不斷地重復下去.如:在字符串
位出現;……;如此不斷地重復下去.如:在字符串![]() 中,子串“
中,子串“![]() ”在第
”在第![]() 位和第
位和第![]() 位出現,而不是在第
位出現,而不是在第![]() 位和第
位和第![]() 位出現.記在
位出現.記在![]() 位由
位由![]() 組成的所有字符串中,子串“
組成的所有字符串中,子串“![]() ”在第
”在第![]() 位出現的字符串的個數為
位出現的字符串的個數為![]() .
.
(1)求![]() 的值;
的值;
(2)求證:對任意的正整數![]() ,
,![]() 是
是![]() 的倍數.
的倍數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生態農場有一矩形地塊,地塊內有一半圓形池塘(如圖所示),其中![]() 百米,
百米,![]() 百米,半圓形池塘的半徑為1百米,圓心
百米,半圓形池塘的半徑為1百米,圓心![]() 與線段
與線段![]() 的中點重合,半圓與
的中點重合,半圓與![]() 的左側交點為
的左側交點為![]() .該農場計劃分別在
.該農場計劃分別在![]() 和
和![]() 上各選一點
上各選一點![]() ,修建道路
,修建道路![]() ,要求
,要求![]() 與半圓相切.
與半圓相切.
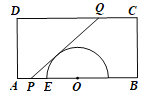
(1)若![]() ,求該道路的總長;
,求該道路的總長;
(2)若![]() 為觀光道路,修建費用是4萬元/百米,
為觀光道路,修建費用是4萬元/百米,![]() 為便道,修建費用是1萬元/百米,求修建觀光道路與便道的總費用的最小值.
為便道,修建費用是1萬元/百米,求修建觀光道路與便道的總費用的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出1t該產品獲利潤500元,未售出的產品,每1t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如右圖所示.經銷商為下一個銷售季度購進了130t該農產品.以x(單位:t,100≤x≤150)表示下一個銷售季度內經銷該農產品的數量,T表示利潤.
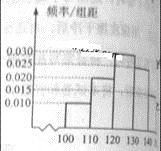
(Ⅰ)將T表示為x的函數
(Ⅱ)根據直方圖估計利潤T不少于57000元的概率;
(Ⅲ)在直方圖的需求量分組中,以各組的區間中點值代表該組的各個值需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若x![]() ,則取x=105,且x=105的概率等于需求量落入[100,110
,則取x=105,且x=105的概率等于需求量落入[100,110![]() ,求T的數學期望.
,求T的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(I)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(II)求證: ![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
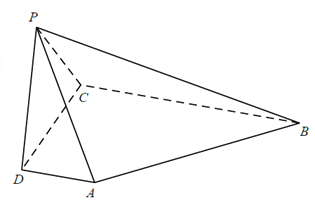
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,人們支付方式發生巨大轉變,使用移動支付購買商品已成為一部分人的消費習慣,某企業為了解該企業員工![]() 兩種移動支付方式的使用情況,從全體員工中隨機抽取了100人,統計了他們在某個月的消費支出情況,發現樣本中
兩種移動支付方式的使用情況,從全體員工中隨機抽取了100人,統計了他們在某個月的消費支出情況,發現樣本中![]() 兩種支付方式都沒有使用過的有5人;使用了
兩種支付方式都沒有使用過的有5人;使用了![]() 兩種方式支付的員工,支付金額和相應人數分布如下表,依據數據估算:若從該公司隨機抽取1名員工,則該員工在該月
兩種方式支付的員工,支付金額和相應人數分布如下表,依據數據估算:若從該公司隨機抽取1名員工,則該員工在該月![]() 兩種支付方式都使用過的概率為_______________
兩種支付方式都使用過的概率為_______________
支付金額(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com