
【題目】已知函數![]() ,
,![]() .
.
(1)求![]() 在點P(1,
在點P(1,![]() )處的切線方程;
)處的切線方程;
(2)若關于x的不等式![]() 有且僅有三個整數解,求實數t的取值范圍;
有且僅有三個整數解,求實數t的取值范圍;
(3)若![]() 存在兩個正實數
存在兩個正實數![]() ,
,![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)求出P(1,0),x>0,![]() ,f′(1)=1,利用導數的幾何意義能求出f(x)在點P(1,f(1))處的切線方程.
,f′(1)=1,利用導數的幾何意義能求出f(x)在點P(1,f(1))處的切線方程.
(2)求出![]() ,x>0,則f′(x)=0,得x=e,列表討論能求出實數t的取值范圍.
,x>0,則f′(x)=0,得x=e,列表討論能求出實數t的取值范圍.
(3)h(x)=x2﹣2x+4lnx,從而(x1+x2)2﹣2(x1+x2)﹣4lnx1x2,令t=x1x2,![]() =t2+2t﹣4lnt,(t>0),…(11分)則
=t2+2t﹣4lnt,(t>0),…(11分)則![]() =2t+2﹣
=2t+2﹣![]() =
=![]() ,由此利用導數性質能證明x1+x2≥3.
,由此利用導數性質能證明x1+x2≥3.
(1)![]() ,
,![]() ,所以
,所以![]() 點坐標為
點坐標為![]() ;
;
又![]() ,
,![]() ,則切線方程為
,則切線方程為![]() ,
,
所以函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(2)![]()
|
|
|
|
| 正 | 0 | 負 |
| 單調增 | 極大值 | 單調減 |
由![]() , 得
, 得![]() ;
;
![]() 時,
時,![]() 或
或![]() ,滿足條件的整數解有無數個,舍;
,滿足條件的整數解有無數個,舍;
![]() 時,
時,![]() ,得
,得![]() 且
且![]() ,滿足條件的整數解有無數個,舍;
,滿足條件的整數解有無數個,舍;
![]() 時,
時,![]() 或
或![]() ,當
,當![]() 時,無整數解;
時,無整數解;
當![]() 時,不等式有且僅有三個整數解,又
時,不等式有且僅有三個整數解,又![]() ,
,![]() ,
,![]()
因為![]() 在
在![]() 遞增,在
遞增,在![]() 遞減;所以
遞減;所以![]() , 即
, 即![]() ,即
,即![]() ;
;
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
(3)![]() ,
,
因為![]() ,
,
所以![]() ,
,
即![]() ,
,
令![]() ,
,![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 時,取得最小值,最小值為3.
時,取得最小值,最小值為3.
因為存在兩個正實數![]() ,滿足
,滿足![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
因為![]() 為正實數,所以
為正實數,所以![]() .
.


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若存在常數
,若存在常數![]() ,使得
,使得![]() 對任意的
對任意的![]() 成立,則稱函數
成立,則稱函數![]() 是“類周期函數”.
是“類周期函數”.
(1)判斷函數![]() ,
,![]() 是否是“類周期函數”,并證明你的結論;
是否是“類周期函數”,并證明你的結論;
(2)求證:若函數![]() 是“類周期函數”,且
是“類周期函數”,且![]() 是偶函數,則
是偶函數,則![]() 是周期函數;
是周期函數;
(3)求證:當![]() 時,函數
時,函數![]() 一定是“類周期函數”.
一定是“類周期函數”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=a-bcos![]() (b>0)的最大值為
(b>0)的最大值為![]() ,最小值為-
,最小值為-![]() .
.
(1)求a,b的值;
(2)求函數g(x)=-4asin![]() 的最小值并求出對應x的集合.
的最小值并求出對應x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() ,如圖1.以
,如圖1.以![]() 為折痕將
為折痕將![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,如圖2.
的位置,如圖2.
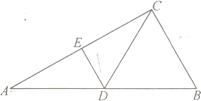
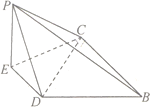
如圖1 如圖2
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海洋藍洞是地球罕見的自然地理現象,被喻為“地球留給人類保留宇宙秘密的最后遺產”,我國擁有世界上最深的海洋藍洞,若要測量如圖所示的藍洞的口徑![]() ,
,![]() 兩點間的距離,現在珊瑚群島上取兩點
兩點間的距離,現在珊瑚群島上取兩點![]() ,
,![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() 兩點的距離為___.
兩點的距離為___.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com